Difference between revisions of "Neumann d-bar problem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex done, typos) |
||
| Line 1: | Line 1: | ||
| − | + | {{TEX|done}} | |
| − | + | ''Neumann DBAR problem, $ \overline \partial \; $- | |
| + | problem, $ \overline \partial \; $- | ||
| + | Neumann problem, DBAR problem, Neumann problem for the Cauchy–Riemann complex'' | ||
| − | + | A non-coercive boundary problem for the complex Laplacian. Let $ M $ | |
| + | be a relatively compact domain of a complex manifold $ M ^{1} $ | ||
| + | of dimension $ n + 1 $ | ||
| + | with smooth boundary $ b M $. | ||
| + | The Cauchy–Riemann operator $ \overline \partial \; $( | ||
| + | defined on functions on a domain $ M \subset \mathbf C ^{n+1} $ | ||
| + | by $ \overline \partial \; f = \sum _{i=1} ^{n+1} ( {\partial f} / {\partial \overline{z}\; _ i} ) \ d \overline{z}\; _{i} $) | ||
| + | naturally extends to define the Dolbeault complex or Cauchy–Riemann complex $$ | ||
| + | 0 \rightarrow \Lambda ^{p,0} (M) \stackrel{ {\overline \partial \;}} \rightarrow \Lambda ^{p,1} (M) \stackrel{ {\overline \partial \;}} \rightarrow \dots \stackrel{ {\overline \partial \;}} \rightarrow | ||
| + | \Lambda ^{p,n+1} (M) \rightarrow 0 , | ||
| + | $$ | ||
| + | where $ \Lambda ^{p,q} (M) $ | ||
| + | is the space of differential forms of type $ ( p ,\ q ) $ | ||
| + | on $ M $. | ||
| + | The holomorphic functions are the solutions of $ \overline \partial \; f = 0 $ | ||
| + | and the inhomogeneous equation $ \overline \partial \; f = \phi $( | ||
| + | under the necessary compactibility condition $ \overline \partial \; \phi = 0 $) | ||
| + | is also of interest. For instance, in connection with the Levi problem: Given $ x \in b M $, | ||
| + | is there a holomorphic function on $ M $ | ||
| + | which blows up at $ x $? | ||
| + | Using a general formalism of D.C. Spencer (and general Hilbert space theory), the problem $ \overline \partial \; f = \phi $ | ||
| + | leads to the $ \overline \partial \; $- | ||
| + | Neumann problem $$ \tag{A1} | ||
| + | ( \overline \partial \; \overline \partial \; {} ^{*} + \overline \partial \; {} ^{*} \overline \partial \; ) u = \phi . | ||
| + | $$ | ||
| + | Here $ \overline \partial \; {} ^{*} $ | ||
| + | is the adjoint of $ \overline \partial \; $, | ||
| + | which is defined by $ \langle \overline \partial \; {} ^{*} f ,\ g \rangle = \langle f ,\ \overline \partial \; g \rangle $, | ||
| + | where the inner product is given by integration with respect to the volume form determined by a given Hermitian metric on $ \overline{M}\; $. | ||
| + | The operator $ \square = \overline \partial \; \overline \partial \; {} ^{*} + \overline \partial \; {} ^{*} \overline \partial \; $ | ||
| + | is called the complex Laplacian. If $ M $ | ||
| + | is a [[Kähler manifold|Kähler manifold]], then $ \square = \Delta /2 $, | ||
| + | where $ \Delta $ | ||
| + | is the usual Laplacian of the de Rham complex, cf. [[De Rham cohomology|de Rham cohomology]]. | ||
| − | + | Strictly speaking, equation (A1) should be written as $$ \tag{A2} | |
| − | + | ( \overline \partial \; _{q} \overline \partial \; {} _{q} ^{*} + \overline \partial \; {} _{q+1} ^{*} \overline \partial \; _{q+1} ) (u) = \phi , | |
| − | + | $$ | |
| − | + | where $ u \in \Lambda ^{p,q+1} (M) $, | |
| − | + | $ \overline \partial \; _{q} : \ \Lambda ^{p,q} (M) \rightarrow \Lambda ^{p,q+1} (M) $, | |
| − | + | $ \overline \partial \; {} _{q} ^{*} : \ \Lambda ^{p,q+1} (M) \rightarrow \Lambda ^{p,q} (M) $; | |
| − | + | $ q = - 1 ,\ 0 \dots n + 1 $, | |
| − | + | $ \Lambda ^{p,-1} (M) = 0 = \Lambda ^{p,n+2} (M) $. | |
| − | + | Thus equation (A2) comes naturally equipped with the boundary conditions $$ \tag{A3} | |
| − | + | u \in \textrm{ Domain } ( \overline \partial \; {} _{q} ^{*} ), | |
| − | + | $$ | |
| − | + | $$ \tag{A4} | |
| − | + | \overline \partial \; _{q+1} u \in \textrm{ Domain } ( \overline \partial \; {} _{q+1} ^{*} ). | |
| − | + | $$( | |
| − | + | The $ \overline \partial \; $- | |
| − | + | Neumann boundary conditions.) The operator $ \square $ | |
| − | + | is elliptic, but the boundary conditions are not. Nevertheless, J.J. Kohn was able to prove existence and to provide a systematic analysis of regularity. A main result is the estimate $$ | |
| − | + | \| u \| _{s+1} \leq A _{s} \| \square u \| _{s} + \| u \| , | |
| − | + | $$ | |
| − | + | where $ \| \cdot \| _{s} $ | |
| − | + | are Sobolev norms (cf. [[Sobolev space|Sobolev space]]). For more details cf. [[#References|[a1]]], [[#References|[a2]]]. A great deal of additional and related material can be found in [[#References|[a1]]]–[[#References|[a4]]]. | |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G.B. Folland, J.J. Kohn, "The Neumann problem for the Cauchy–Riemann complex" , ''Annals Math. Studies'' , '''75''' , Princeton Univ. Press (1972)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P.C. Greiner, E.M. Sfein, "Estimates for the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066410/n06641047.png" />-Neumann problem" , Princeton Univ. Press (1977)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> F. Trèves, "Introduction to pseudodifferential and Fourier integral operators" , '''1''' , Plenum (1980) pp. Sect. III.8</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J.J. Kohn, "Methods of partial differential equations in complex analysis" R.O. Wells jr. (ed.) , ''Several Complex Variables'' , '''1''' , Amer. Math. Soc. (1977) pp. 215–240</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G.B. Folland, J.J. Kohn, "The Neumann problem for the Cauchy–Riemann complex" , ''Annals Math. Studies'' , '''75''' , Princeton Univ. Press (1972)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P.C. Greiner, E.M. Sfein, "Estimates for the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066410/n06641047.png" />-Neumann problem" , Princeton Univ. Press (1977)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> F. Trèves, "Introduction to pseudodifferential and Fourier integral operators" , '''1''' , Plenum (1980) pp. Sect. III.8</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J.J. Kohn, "Methods of partial differential equations in complex analysis" R.O. Wells jr. (ed.) , ''Several Complex Variables'' , '''1''' , Amer. Math. Soc. (1977) pp. 215–240</TD></TR></table> | ||
Latest revision as of 10:21, 22 December 2019
Neumann DBAR problem, $ \overline \partial \; $-
problem, $ \overline \partial \; $-
Neumann problem, DBAR problem, Neumann problem for the Cauchy–Riemann complex
A non-coercive boundary problem for the complex Laplacian. Let $ M $ be a relatively compact domain of a complex manifold $ M ^{1} $ of dimension $ n + 1 $ with smooth boundary $ b M $. The Cauchy–Riemann operator $ \overline \partial \; $( defined on functions on a domain $ M \subset \mathbf C ^{n+1} $ by $ \overline \partial \; f = \sum _{i=1} ^{n+1} ( {\partial f} / {\partial \overline{z}\; _ i} ) \ d \overline{z}\; _{i} $) naturally extends to define the Dolbeault complex or Cauchy–Riemann complex $$ 0 \rightarrow \Lambda ^{p,0} (M) \stackrel{ {\overline \partial \;}} \rightarrow \Lambda ^{p,1} (M) \stackrel{ {\overline \partial \;}} \rightarrow \dots \stackrel{ {\overline \partial \;}} \rightarrow \Lambda ^{p,n+1} (M) \rightarrow 0 , $$ where $ \Lambda ^{p,q} (M) $ is the space of differential forms of type $ ( p ,\ q ) $ on $ M $. The holomorphic functions are the solutions of $ \overline \partial \; f = 0 $ and the inhomogeneous equation $ \overline \partial \; f = \phi $( under the necessary compactibility condition $ \overline \partial \; \phi = 0 $) is also of interest. For instance, in connection with the Levi problem: Given $ x \in b M $, is there a holomorphic function on $ M $ which blows up at $ x $? Using a general formalism of D.C. Spencer (and general Hilbert space theory), the problem $ \overline \partial \; f = \phi $ leads to the $ \overline \partial \; $- Neumann problem $$ \tag{A1} ( \overline \partial \; \overline \partial \; {} ^{*} + \overline \partial \; {} ^{*} \overline \partial \; ) u = \phi . $$ Here $ \overline \partial \; {} ^{*} $ is the adjoint of $ \overline \partial \; $, which is defined by $ \langle \overline \partial \; {} ^{*} f ,\ g \rangle = \langle f ,\ \overline \partial \; g \rangle $, where the inner product is given by integration with respect to the volume form determined by a given Hermitian metric on $ \overline{M}\; $. The operator $ \square = \overline \partial \; \overline \partial \; {} ^{*} + \overline \partial \; {} ^{*} \overline \partial \; $ is called the complex Laplacian. If $ M $ is a Kähler manifold, then $ \square = \Delta /2 $, where $ \Delta $ is the usual Laplacian of the de Rham complex, cf. de Rham cohomology.
Strictly speaking, equation (A1) should be written as $$ \tag{A2} ( \overline \partial \; _{q} \overline \partial \; {} _{q} ^{*} + \overline \partial \; {} _{q+1} ^{*} \overline \partial \; _{q+1} ) (u) = \phi , $$ where $ u \in \Lambda ^{p,q+1} (M) $, $ \overline \partial \; _{q} : \ \Lambda ^{p,q} (M) \rightarrow \Lambda ^{p,q+1} (M) $, $ \overline \partial \; {} _{q} ^{*} : \ \Lambda ^{p,q+1} (M) \rightarrow \Lambda ^{p,q} (M) $; $ q = - 1 ,\ 0 \dots n + 1 $, $ \Lambda ^{p,-1} (M) = 0 = \Lambda ^{p,n+2} (M) $. Thus equation (A2) comes naturally equipped with the boundary conditions $$ \tag{A3} u \in \textrm{ Domain } ( \overline \partial \; {} _{q} ^{*} ), $$ $$ \tag{A4} \overline \partial \; _{q+1} u \in \textrm{ Domain } ( \overline \partial \; {} _{q+1} ^{*} ). $$( The $ \overline \partial \; $- Neumann boundary conditions.) The operator $ \square $ is elliptic, but the boundary conditions are not. Nevertheless, J.J. Kohn was able to prove existence and to provide a systematic analysis of regularity. A main result is the estimate $$ \| u \| _{s+1} \leq A _{s} \| \square u \| _{s} + \| u \| , $$ where $ \| \cdot \| _{s} $ are Sobolev norms (cf. Sobolev space). For more details cf. [a1], [a2]. A great deal of additional and related material can be found in [a1]–[a4].
References
| [a1] | G.B. Folland, J.J. Kohn, "The Neumann problem for the Cauchy–Riemann complex" , Annals Math. Studies , 75 , Princeton Univ. Press (1972) |
| [a2] | P.C. Greiner, E.M. Sfein, "Estimates for the 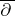 -Neumann problem" , Princeton Univ. Press (1977) -Neumann problem" , Princeton Univ. Press (1977) |
| [a3] | F. Trèves, "Introduction to pseudodifferential and Fourier integral operators" , 1 , Plenum (1980) pp. Sect. III.8 |
| [a4] | J.J. Kohn, "Methods of partial differential equations in complex analysis" R.O. Wells jr. (ed.) , Several Complex Variables , 1 , Amer. Math. Soc. (1977) pp. 215–240 |
Neumann d-bar problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Neumann_d-bar_problem&oldid=44321