Negative variation of a function
From Encyclopedia of Mathematics
negative increment of a function
One of the two terms whose sum is the complete increment or variation of a function on a given interval. Let 
be a function of a real variable, defined on an interval 
and taking finite real values.
Let 
be an arbitrary partition of 
and let
 |
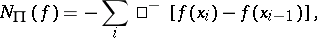where the summation is over those numbers 
for which the difference 
is non-positive. The quantity
 |
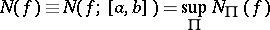is called the negative variation (negative increment) of the function 
on the interval 
. It is always true that 
. See also Positive variation of a function; Variation of a function.
References
| [1] | H. Lebesgue, "Leçons sur l'intégration et la récherche des fonctions primitives" , Gauthier-Villars (1928) |
How to Cite This Entry:
Negative variation of a function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Negative_variation_of_a_function&oldid=13979
Negative variation of a function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Negative_variation_of_a_function&oldid=13979
This article was adapted from an original article by B.I. Golubov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article