Negative binomial distribution
A probability distribution of a random variable 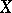 which takes non-negative integer values
which takes non-negative integer values 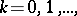 in accordance with the formula
in accordance with the formula
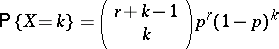 | (*) |
for any real values of the parameters  and
and 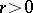 . The generating function and the characteristic function of a negative binomial distribution are defined by the formulas
. The generating function and the characteristic function of a negative binomial distribution are defined by the formulas
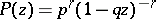 |
and
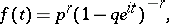 |
respectively, where  . The mathematical expectation and variance are equal, respectively, to
. The mathematical expectation and variance are equal, respectively, to 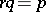 and
and 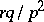 . The distribution function of a negative binomial distribution for the values
. The distribution function of a negative binomial distribution for the values 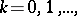 is defined in terms of the values of the beta-distribution function at a point
is defined in terms of the values of the beta-distribution function at a point 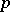 by the following relation:
by the following relation:
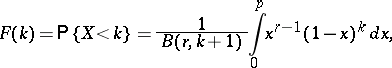 |
where 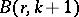 is the beta-function.
is the beta-function.
The origin of the term "negative binomial distribution" is explained by the fact that this distribution is generated by a binomial with a negative exponent, i.e. the probabilities (*) are the coefficients of the expansion of 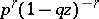 in powers of
in powers of  .
.
Negative binomial distributions are encountered in many applications of probability theory. For an integer 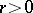 , the negative binomial distribution is interpreted as the distribution of the number of failures before the
, the negative binomial distribution is interpreted as the distribution of the number of failures before the  -th "success" in a scheme of Bernoulli trials with probability of "success"
-th "success" in a scheme of Bernoulli trials with probability of "success" 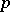 ; in this context it is usually called a Pascal distribution and is a discrete analogue of the gamma-distribution. When
; in this context it is usually called a Pascal distribution and is a discrete analogue of the gamma-distribution. When 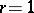 , the negative binomial distribution coincides with the geometric distribution. The negative binomial distribution often appears in problems related to the randomization of the parameters of a distribution; for example, if
, the negative binomial distribution coincides with the geometric distribution. The negative binomial distribution often appears in problems related to the randomization of the parameters of a distribution; for example, if 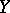 is a random variable having, conditionally on
is a random variable having, conditionally on 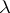 , a Poisson distribution with random parameter
, a Poisson distribution with random parameter 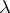 , which in turn has a gamma-distribution with density
, which in turn has a gamma-distribution with density
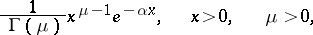 |
then the marginal distribution of 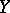 will be a negative binomial distribution with parameters
will be a negative binomial distribution with parameters 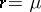 and
and 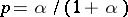 . The negative binomial distribution serves as a limiting form of a Pólya distribution.
. The negative binomial distribution serves as a limiting form of a Pólya distribution.
The sum of independent random variables 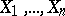 which have negative binomial distributions with parameters
which have negative binomial distributions with parameters 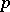 and
and  , respectively, has a negative binomial distribution with parameters
, respectively, has a negative binomial distribution with parameters 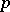 and
and 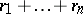 . For large
. For large  and small
and small 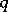 , where
, where 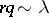 , the negative binomial distribution is approximated by the Poisson distribution with parameter
, the negative binomial distribution is approximated by the Poisson distribution with parameter 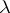 . Many properties of a negative binomial distribution are determined by the fact that it is a generalized Poisson distribution.
. Many properties of a negative binomial distribution are determined by the fact that it is a generalized Poisson distribution.
References
| [1] | W. Feller, "An introduction to probability theory and its applications" , 1–2 , Wiley (1950–1966) |
Comments
See also Binomial distribution.
References
| [a1] | N.L. Johnson, S. Kotz, "Distributions in statistics, discrete distributions" , Wiley (1969) |
Negative binomial distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Negative_binomial_distribution&oldid=18065