Difference between revisions of "Multiplier theory"
m (links) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | m0655301.png | ||
| + | $#A+1 = 29 n = 1 | ||
| + | $#C+1 = 29 : ~/encyclopedia/old_files/data/M065/M.0605530 Multiplier theory | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | Given a [[Fourier series|Fourier series]] on $ [ - \pi , \pi ) $, | ||
| + | $ \sum _ {n = - \infty } ^ \infty c _ {n} e ^ {inx} $ | ||
| + | say, and a (doubly infinite) sequence $ \{ \lambda _ {n} \} $, | ||
| + | one may form a new Fourier series, $ \sum _ {n = - \infty } ^ \infty \lambda _ {n} c _ {n} e ^ {inx} $. | ||
| + | The sequence $ \{ \lambda _ {n} \} $ | ||
| + | is called a Fourier multiplier. The principal problem about Fourier multipliers is to determine conditions on $ \{ \lambda _ {n} \} $ | ||
| + | which guarantee that, when the old Fourier series corresponds to an element of some space $ {\mathcal E} $ | ||
| + | of functions or generalized functions (cf. [[Generalized function|Generalized function]]) on $ [ - \pi , \pi ) $, | ||
| + | then the new series corresponds to an element of some other given space $ {\mathcal F} $ | ||
| + | of functions or generalized functions on $ [ \pi , \pi ) $. | ||
| + | Typically, $ {\mathcal E} $ | ||
| + | and $ {\mathcal F} $ | ||
| + | are Lebesgue spaces, Sobolev spaces or similar function spaces (cf. [[Lebesgue space|Lebesgue space]]; [[Sobolev space|Sobolev space]]). Particular cases of the problem were first solved by W.H. Young (1913), H. Steinhaus (1915) and S. Sidon (1921), the most significant of these solutions being that $ \{ \lambda _ {n} \} $ | ||
| + | is a multiplier from the space of integrable functions to itself or from the space of continuous functions to itself if and only if $ \sum _ {n = - \infty } ^ \infty \lambda _ {n} e ^ {inx} $ | ||
| + | is a [[Fourier–Stieltjes series|Fourier–Stieltjes series]]. Equivalently, one can seek to characterize generalized functions $ \phi $ | ||
| + | on $ [ - \pi , \pi ) $ | ||
| + | with the property that, if $ f \in {\mathcal E} $, | ||
| + | then the convolution product $ \phi \star f \in {\mathcal F} $; | ||
| + | the corresponding Fourier multiplier is the sequence of Fourier coefficients of $ \phi $. | ||
The analogous problem, of characterizing operators which map one space to another and which correspond to a [[pointwise multiplication]] of the Fourier transform by a fixed object, can be posed in the context of Fourier integrals rather than series, and in one or several variables. (Indeed, the theory can even be developed in the general context of locally compact groups.) | The analogous problem, of characterizing operators which map one space to another and which correspond to a [[pointwise multiplication]] of the Fourier transform by a fixed object, can be posed in the context of Fourier integrals rather than series, and in one or several variables. (Indeed, the theory can even be developed in the general context of locally compact groups.) | ||
| − | The most important results on Fourier multipliers are connected with the theories of singular integral operators and pseudo-differential operators (cf. [[Pseudo-differential operator|Pseudo-differential operator]]). The general style of these is exemplified by the theorem that a bounded function | + | The most important results on Fourier multipliers are connected with the theories of singular integral operators and pseudo-differential operators (cf. [[Pseudo-differential operator|Pseudo-differential operator]]). The general style of these is exemplified by the theorem that a bounded function $ m $ |
| + | on $ \mathbf R $ | ||
| + | whose total variation (cf. [[Variation of a function]]) on each dyadic interval $ \pm [ 2 ^ {k} , 2 ^ {k+} 1 ] $ | ||
| + | is bounded is a Fourier $ L _ {p} $- | ||
| + | multiplier (i.e. the associated operator maps $ L _ {p} ( \mathbf R ) $ | ||
| + | into itself) if $ 1 < p < \infty $. | ||
| + | Perhaps the other most important result in the field is C. Fefferman's theorem that in $ \mathbf R ^ {n} $, | ||
| + | where $ n \geq 2 $, | ||
| + | the characteristic function of the unit ball is a Fourier $ L _ {p} $- | ||
| + | multiplier only if $ p = 2 $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Hörmander, "Estimates for translation-invariant operators in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065530/m06553030.png" /> spaces" ''Acta Math.'' , '''104''' (1960) pp. 93–139</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> C. Fefferman, "The multiplier problem for the ball" ''Ann. of Math.'' , '''94''' (1971) pp. 330–336</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A. Zygmund, "Trigonometric series" , '''2''' , Cambridge Univ. Press (1988)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Hörmander, "Estimates for translation-invariant operators in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065530/m06553030.png" /> spaces" ''Acta Math.'' , '''104''' (1960) pp. 93–139</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> C. Fefferman, "The multiplier problem for the ball" ''Ann. of Math.'' , '''94''' (1971) pp. 330–336</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A. Zygmund, "Trigonometric series" , '''2''' , Cambridge Univ. Press (1988)</TD></TR></table> | ||
Latest revision as of 08:02, 6 June 2020
Given a Fourier series on $ [ - \pi , \pi ) $,
$ \sum _ {n = - \infty } ^ \infty c _ {n} e ^ {inx} $
say, and a (doubly infinite) sequence $ \{ \lambda _ {n} \} $,
one may form a new Fourier series, $ \sum _ {n = - \infty } ^ \infty \lambda _ {n} c _ {n} e ^ {inx} $.
The sequence $ \{ \lambda _ {n} \} $
is called a Fourier multiplier. The principal problem about Fourier multipliers is to determine conditions on $ \{ \lambda _ {n} \} $
which guarantee that, when the old Fourier series corresponds to an element of some space $ {\mathcal E} $
of functions or generalized functions (cf. Generalized function) on $ [ - \pi , \pi ) $,
then the new series corresponds to an element of some other given space $ {\mathcal F} $
of functions or generalized functions on $ [ \pi , \pi ) $.
Typically, $ {\mathcal E} $
and $ {\mathcal F} $
are Lebesgue spaces, Sobolev spaces or similar function spaces (cf. Lebesgue space; Sobolev space). Particular cases of the problem were first solved by W.H. Young (1913), H. Steinhaus (1915) and S. Sidon (1921), the most significant of these solutions being that $ \{ \lambda _ {n} \} $
is a multiplier from the space of integrable functions to itself or from the space of continuous functions to itself if and only if $ \sum _ {n = - \infty } ^ \infty \lambda _ {n} e ^ {inx} $
is a Fourier–Stieltjes series. Equivalently, one can seek to characterize generalized functions $ \phi $
on $ [ - \pi , \pi ) $
with the property that, if $ f \in {\mathcal E} $,
then the convolution product $ \phi \star f \in {\mathcal F} $;
the corresponding Fourier multiplier is the sequence of Fourier coefficients of $ \phi $.
The analogous problem, of characterizing operators which map one space to another and which correspond to a pointwise multiplication of the Fourier transform by a fixed object, can be posed in the context of Fourier integrals rather than series, and in one or several variables. (Indeed, the theory can even be developed in the general context of locally compact groups.)
The most important results on Fourier multipliers are connected with the theories of singular integral operators and pseudo-differential operators (cf. Pseudo-differential operator). The general style of these is exemplified by the theorem that a bounded function $ m $ on $ \mathbf R $ whose total variation (cf. Variation of a function) on each dyadic interval $ \pm [ 2 ^ {k} , 2 ^ {k+} 1 ] $ is bounded is a Fourier $ L _ {p} $- multiplier (i.e. the associated operator maps $ L _ {p} ( \mathbf R ) $ into itself) if $ 1 < p < \infty $. Perhaps the other most important result in the field is C. Fefferman's theorem that in $ \mathbf R ^ {n} $, where $ n \geq 2 $, the characteristic function of the unit ball is a Fourier $ L _ {p} $- multiplier only if $ p = 2 $.
References
| [a1] | L. Hörmander, "Estimates for translation-invariant operators in 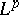 spaces" Acta Math. , 104 (1960) pp. 93–139 spaces" Acta Math. , 104 (1960) pp. 93–139 |
| [a2] | C. Fefferman, "The multiplier problem for the ball" Ann. of Math. , 94 (1971) pp. 330–336 |
| [a3] | A. Zygmund, "Trigonometric series" , 2 , Cambridge Univ. Press (1988) |
Multiplier theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multiplier_theory&oldid=35256