Multiplicity of a weight
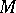 of a representation
of a representation 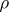 of a Lie algebra
of a Lie algebra 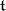 in a finite-dimensional vector space
in a finite-dimensional vector space 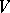
The dimension 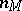 of the weight subspace
of the weight subspace 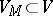 corresponding to the weight
corresponding to the weight 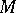 (see Weight of a representation of a Lie algebra).
(see Weight of a representation of a Lie algebra).
Let 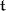 be a Cartan subalgebra of a semi-simple Lie algebra
be a Cartan subalgebra of a semi-simple Lie algebra 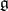 over an algebraically closed field of characteristic zero, and let
over an algebraically closed field of characteristic zero, and let  be the restriction to
be the restriction to 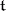 of a finite-dimensional representation
of a finite-dimensional representation 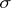 of the algebra
of the algebra 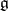 . In this case the space
. In this case the space 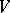 is the direct sum of the weight subspaces of
is the direct sum of the weight subspaces of 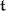 corresponding to the different weights. These weights and their multiplicities are often called the weights and the multiplicities of the representation
corresponding to the different weights. These weights and their multiplicities are often called the weights and the multiplicities of the representation 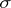 of the algebra
of the algebra  .
.
Suppose that 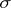 is an irreducible representation and let
is an irreducible representation and let 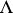 be its highest weight (see Cartan theorem on the highest weight vector). Then
be its highest weight (see Cartan theorem on the highest weight vector). Then 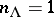 . Various devices are available for computing the multiplicities of weights other than the highest weight. Two of these are classical results in representation theory: Freudenthal's formula and Kostant's formula.
. Various devices are available for computing the multiplicities of weights other than the highest weight. Two of these are classical results in representation theory: Freudenthal's formula and Kostant's formula.
1) Freudenthal's formula (see , [1]). Let  be the natural scalar product on the space
be the natural scalar product on the space 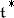 adjoint to
adjoint to 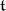 , induced by the Killing form on
, induced by the Killing form on 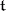 ; let
; let 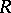 be the root system of the algebra
be the root system of the algebra 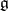 relative to
relative to  and let
and let 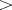 be a partial order relation on
be a partial order relation on 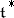 determined by some fixed system of simple roots
determined by some fixed system of simple roots  in
in 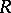 . Then
. Then
 |
 |
where  and by definition
and by definition 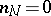 if
if 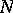 is not a weight of the representation
is not a weight of the representation 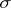 . For any weight
. For any weight 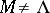 , the coefficient of
, the coefficient of 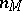 on the left of the formula is different from zero. This formula is essentially a recurrence formula: it enables one to express
on the left of the formula is different from zero. This formula is essentially a recurrence formula: it enables one to express 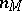 in terms of
in terms of 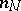 for
for 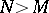 . Since it is known that
. Since it is known that 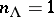 , Freudenthal's formula yields an effective method for the computation of the multiplicities
, Freudenthal's formula yields an effective method for the computation of the multiplicities 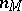 .
.
2) Kostant's formula (see [5], [1]). Let 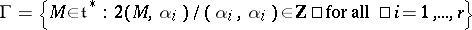 . This set
. This set 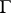 is a multiplicative subgroup in
is a multiplicative subgroup in 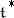 which is invariant under the Weyl group
which is invariant under the Weyl group  , which acts on
, which acts on 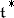 in a natural way. The element
in a natural way. The element 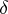 — and indeed all weights of the representation
— and indeed all weights of the representation 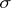 — are members of
— are members of 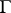 . Suppose that for each
. Suppose that for each 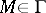 the number
the number  is the number of solutions
is the number of solutions 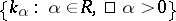 of the equation
of the equation
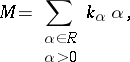 |
where 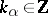 ,
, 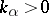 for all
for all 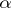 . The function
. The function 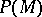 on
on 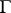 is known as the partition function. Then
is known as the partition function. Then
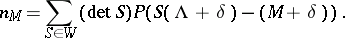 |
Practical application of the above formulas involves cumbersome computations. For semi-simple algebras of rank 2, there are more convenient geometrical rules for evaluating the multiplicity of a weight (see [2]).
References
| [1] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) |
| [2] | D.P. Zhelobenko, "Lectures on the theory of Lie groups" , Dubna (1965) (In Russian) |
| [3] | D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) |
| [4a] | H. Freudenthal, "Zur Berechnung der Charaktere der halbeinfacher Liescher Gruppen I" Indag. Math. , 16 (1954) pp. 369–376 |
| [4b] | H. Freudenthal, "Zur Berechnung der Charaktere der halbeinfacher Liescher Gruppen II" Indag. Math. , 16 (1954) pp. 487–491 |
| [4c] | H. Freudenthal, "Zur Berechnung der Charaktere der halbeinfacher Liescher Gruppen III" Indag. Math. , 18 (1956) pp. 511–514 |
| [5] | B. Kostant, "A formula for the multiplicity of a weight" Trans. Amer. Math. Soc. , 93 (1959) pp. 53–73 |
Comments
There is a faster algorithm for computing the full set of weights and multiplicities, due to M. Demazure [a3].
References
| [a1] | H. Freudenthal, H. de Vries, "Linear Lie groups" , Acad. Press (1969) |
| [a2] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) pp. §5.4 |
| [a3] | M. Demazure, "Une nouvelle formule des charactères" Bull. Sci. Math. (2) , 98 (1974) pp. 163–172 |
Multiplicity of a weight. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multiplicity_of_a_weight&oldid=47938