Morse surgery
surgery
A transformation of smooth manifolds to which the level manifold of a smooth function is subjected on passage through a non-degenerate critical point; it is the most important construction in the topology of manifolds.
Let 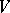 be a smooth
be a smooth  -dimensional manifold (without boundary) in which a
-dimensional manifold (without boundary) in which a 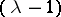 -dimensional sphere
-dimensional sphere 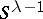 is (smoothly) imbedded. Suppose that the normal bundle of
is (smoothly) imbedded. Suppose that the normal bundle of 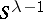 in
in 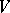 is trivial, that is, a closed tubular neighbourhood
is trivial, that is, a closed tubular neighbourhood 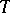 of
of 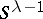 in
in 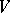 decomposes into a direct product
decomposes into a direct product 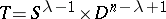 , where
, where 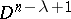 is a disc of dimension
is a disc of dimension 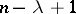 . After having chosen such a decomposition, remove the interior of
. After having chosen such a decomposition, remove the interior of 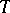 from
from 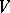 . A manifold is obtained whose boundary decomposes into a product
. A manifold is obtained whose boundary decomposes into a product 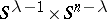 of spheres. But the manifold
of spheres. But the manifold 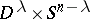 has precisely the same boundary. Identifying the boundaries of
has precisely the same boundary. Identifying the boundaries of 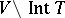 and
and 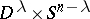 by a diffeomorphism preserving the product structure of
by a diffeomorphism preserving the product structure of 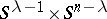 , a manifold
, a manifold 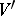 without boundary is again obtained. It is called the result of surgery of
without boundary is again obtained. It is called the result of surgery of 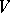 along
along 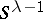 .
.
In the realization of a surgery it is necessary to give a decomposition of the neighbourhood 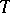 of
of 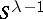 into a direct product, that is, a trivialization of the normal bundle of
into a direct product, that is, a trivialization of the normal bundle of  in
in 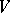 ; in this connection different trivializations (riggings) may give essentially distinct (even homotopically) manifolds
; in this connection different trivializations (riggings) may give essentially distinct (even homotopically) manifolds 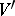 .
.
The number 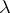 is called the index of the surgery, and the pair
is called the index of the surgery, and the pair 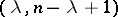 its type. If
its type. If 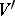 is obtained from
is obtained from 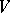 by a surgery of type
by a surgery of type 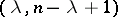 , then
, then  is obtained from
is obtained from  by a surgery of type
by a surgery of type 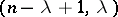 . For
. For 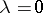 ,
, 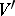 is a disjoint union of
is a disjoint union of 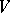 (which may be empty) and
(which may be empty) and 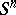 . The construction of a surgery may also be carried out for piecewise-linear and topological manifolds.
. The construction of a surgery may also be carried out for piecewise-linear and topological manifolds.
Example. For 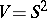 and
and 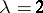 the result of surgery is a disjoint union of spheres, and for
the result of surgery is a disjoint union of spheres, and for 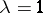 a torus. For
a torus. For 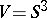 and
and  the product
the product 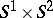 is obtained. The case
is obtained. The case 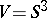 and
and 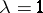 is more complicated: if
is more complicated: if 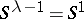 is imbedded in
is imbedded in 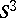 in the standard way (as a great circle), then, depending on the choice of the trivialization of the normal bundle, all lens spaces (cf. Lens space) are obtained; if, however, a knotting of
in the standard way (as a great circle), then, depending on the choice of the trivialization of the normal bundle, all lens spaces (cf. Lens space) are obtained; if, however, a knotting of 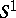 is allowed, then a still larger set of three-dimensional manifolds is obtained.
is allowed, then a still larger set of three-dimensional manifolds is obtained.
If 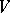 is the boundary of an
is the boundary of an 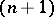 -dimensional manifold
-dimensional manifold 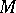 , then
, then 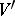 will be the boundary of the manifold
will be the boundary of the manifold 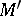 obtained from
obtained from 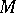 by glueing a handle of the index of
by glueing a handle of the index of 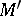 . In particular, if
. In particular, if 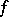 is a smooth function on
is a smooth function on 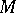 and if
and if 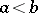 are numbers such that
are numbers such that 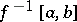 is compact and contains a unique non-degenerate critical point
is compact and contains a unique non-degenerate critical point  , then
, then 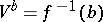 is obtained from
is obtained from 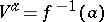 by a surgery of index
by a surgery of index 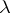 , where
, where 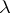 is the Morse index of
is the Morse index of 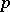 . In a more general form, any surgery
. In a more general form, any surgery 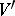 of a manifold
of a manifold 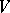 of index
of index 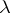 defines a bordism (cobordism)
defines a bordism (cobordism) 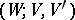 (obtained from the product
(obtained from the product 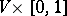 by glueing a handle of index
by glueing a handle of index  to its "right-hand boundary"
to its "right-hand boundary" 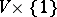 ), and on the triple
), and on the triple 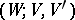 there is a Morse function with a unique critical point of index
there is a Morse function with a unique critical point of index 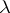 ; moreover, any bordism
; moreover, any bordism 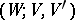 on which there is such a Morse function is obtained in this way. Hence (and from the existence of Morse functions on triples) it follows that two manifolds are bordant if one can be obtained from the other by a sequence of surgeries.
on which there is such a Morse function is obtained in this way. Hence (and from the existence of Morse functions on triples) it follows that two manifolds are bordant if one can be obtained from the other by a sequence of surgeries.
With the known precautions on the treatment of orientations, the result of a surgery on an oriented manifold is again an oriented manifold. In general, for any structure series 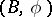 (see
(see 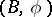 -structure) it is possible to define the idea of
-structure) it is possible to define the idea of 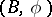 -surgery; in this connection, two manifolds are
-surgery; in this connection, two manifolds are 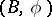 -bordant if they are connected by a finite sequence of
-bordant if they are connected by a finite sequence of 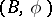 -surgeries.
-surgeries.
The important role of surgery in the topology of manifolds is explained by the fact that it allows one to "delicately" (without infringing on the various properties of manifolds) kill "superfluous" homotopy groups (the operation usually used to this end in homotopy theory, i.e. the operation of "glueing" cells, instantaneously leads out of the class of manifolds). In practice, all theorems on the classification of structures on manifolds are based on the question: Given a mapping 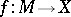 of a closed manifold
of a closed manifold 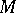 into a CW-complex
into a CW-complex 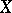 , when does there exist a bordism
, when does there exist a bordism 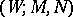 and a mapping
and a mapping  such that
such that 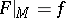 and
and 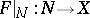 is a homotopy equivalence. The natural route to the solution of this problem is to annihilate the kernels of the homomorphisms
is a homotopy equivalence. The natural route to the solution of this problem is to annihilate the kernels of the homomorphisms 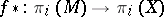 by a sequence of surgeries (where
by a sequence of surgeries (where 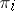 are the homotopy groups). If this succeeds, the resulting mapping will be a homotopy equivalence. The study of the corresponding obstructions (lying in the so-called Wall groups, see [4] and Wall group) is one of the most important stimuli in the development of algebraic
are the homotopy groups). If this succeeds, the resulting mapping will be a homotopy equivalence. The study of the corresponding obstructions (lying in the so-called Wall groups, see [4] and Wall group) is one of the most important stimuli in the development of algebraic 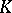 -theory.
-theory.
References
| [1] | M. Morse, "The calculus of variations in the large" , Amer. Math. Soc. (1934) |
| [2] | S.P. Novikov, "Homotopically equivalent smooth manifolds I" Transl. Amer. Math. Soc. , 48 (1965) pp. 271–396 Izv. Akad. Nauk SSSR Ser. Mat. , 28 : 2 (1964) pp. 365–474 |
| [3] | M.A. Kervaire, J.W. Milnor, "Groups of homotopy spheres: I" Ann. of Math. , 77 (1963) pp. 504–537 |
| [4] | A.S. Mishchenko, "Hermitian 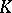 -theory. The theory of characteristic classes and methods of functional analysis" Russian Math. Surveys , 31 : 2 (1976) pp. 71–138 Uspekhi Mat. Nauk , 31 : 2 (1976) pp. 69–134 -theory. The theory of characteristic classes and methods of functional analysis" Russian Math. Surveys , 31 : 2 (1976) pp. 71–138 Uspekhi Mat. Nauk , 31 : 2 (1976) pp. 69–134 |
Comments
There are clear relations between surgery and Morse theory, as indicated above, which is why in the Russian literature the term Morse surgery is frequently used. In the Western literature one simply speaks of surgery. The construction was invented by J.W. Milnor ([a4]).
References
| [a1] | W.B. Browder, "Surgery on simply-connected manifolds" , Springer (1972) |
| [a2] | C.T.C. Wall, "Surgery on compact manifolds" , Acad. Press (1970) |
| [a3] | C.T.-C. Wall, "Surgery on non-simply connected manifolds" Ann. of Math. , 84 (1966) pp. 217–276 |
| [a4] | J.W. Milnor, "A procedure for killing the homotopy groups of differentiable manifolds" , Differential geometry , Proc. Symp. Pure Math. , 3 , Amer. Math. Soc. (1961) pp. 39–55 |
| [a5] | J.W. Milnor, "Morse theory" , Princeton Univ. Press (1963) |
| [a6] | M.W. Hirsch, "Differential topology" , Springer (1976) pp. Chapt. 5, Sect. 3 |
Morse surgery. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Morse_surgery&oldid=24110