Montel theorem
Montel's theorem on the approximation of analytic functions by polynomials: If 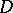 is an open set in the complex
is an open set in the complex  -plane not containing
-plane not containing 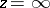 and
and 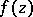 is a single-valued function, analytic at each point
is a single-valued function, analytic at each point 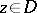 , then there is a sequence of polynomials
, then there is a sequence of polynomials 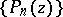 converging to
converging to 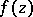 at each
at each 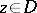 . This theorem is one of the basic results in the theory of approximation of functions of a complex variable; it was obtained by P. Montel .
. This theorem is one of the basic results in the theory of approximation of functions of a complex variable; it was obtained by P. Montel .
Montel's theorem on compactness conditions for a family of holomorphic functions (principle of compactness, see ): Let 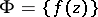 be an infinite family of holomorphic functions in a domain
be an infinite family of holomorphic functions in a domain 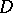 of the complex
of the complex  -plane, then
-plane, then  is pre-compact, that is, any subsequence
is pre-compact, that is, any subsequence  has a subsequence converging uniformly on compact subsets of
has a subsequence converging uniformly on compact subsets of 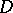 , if
, if 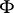 is uniformly bounded in
is uniformly bounded in 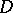 . This theorem can be generalized to a domain
. This theorem can be generalized to a domain 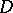 in
in 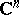 ,
, 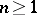 (see Compactness principle).
(see Compactness principle).
Montel's theorem on conditions for normality of a family of holomorphic functions (principle of normality, see [2]): Let 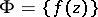 be an infinite family of holomorphic functions in a domain
be an infinite family of holomorphic functions in a domain 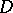 of the complex
of the complex  -plane. If there are two distinct values
-plane. If there are two distinct values  and
and 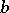 that are not taken by any of the functions
that are not taken by any of the functions  , then
, then 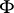 is a normal family, that is, any sequence
is a normal family, that is, any sequence  has a sequence uniformly converging on compact subsets of
has a sequence uniformly converging on compact subsets of 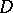 to a holomorphic function or to
to a holomorphic function or to 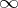 . The conditions of this theorem can be somewhat weakened: It suffices that all
. The conditions of this theorem can be somewhat weakened: It suffices that all 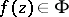 do not take one of the values, say
do not take one of the values, say  , and that the other value
, and that the other value  is taken at most
is taken at most 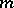 times,
times, 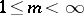 . This theorem can be generalized to a domain
. This theorem can be generalized to a domain 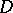 in
in 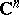 ,
, 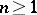 .
.
References
| [1] | P. Montel, "Leçons sur les séries de polynomes à une variable complexe" , Gauthier-Villars (1910) |
| [2] | P. Montel, "Leçons sur les familles normales de fonctions analytiques et leurs applications" , Gauthier-Villars (1927) |
Comments
References
| [a1] | A.I. Markushevich, "Theory of functions of a complex variable" , 3, Sect. 11; 1, Sect. 86; 3, Sect. 50 , Chelsea (1977) (Translated from Russian) |
Montel theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Montel_theorem&oldid=19316