Minimal ideal
A minimal element of the partially ordered set of ideals of a given type of some algebraic system. Since the ordering on the set of ideals is defined by the inclusion relation, a minimal ideal is an ideal not containing ideals of the same type different from itself. For multi-operator groups (in particular, rings) and for lattices, in contrast to semi-groups, it is always assumed that the partially ordered set of ideals does not contain the zero ideal. If no class of ideals is specifically mentioned, a minimal ideal is taken to be minimal in the set of all (non-zero) two-sided ideals.
A minimal two-sided ideal, if one exists, in a semi-group 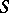 is unique and is the smallest two-sided ideal: it is called the kernel of the semi-group
is unique and is the smallest two-sided ideal: it is called the kernel of the semi-group 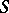 . Not every semi-group has a kernel (for example, an infinite monogenic semi-group) but, for example, the kernel exists in any finite semi-group. The kernel is an ideally-simple semi-group (see Simple semi-group). If the kernel of a semi-group
. Not every semi-group has a kernel (for example, an infinite monogenic semi-group) but, for example, the kernel exists in any finite semi-group. The kernel is an ideally-simple semi-group (see Simple semi-group). If the kernel of a semi-group 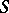 is a group, then
is a group, then 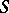 is called a homogroup. A semi-group
is called a homogroup. A semi-group 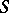 is a homogroup if and only if there is an element
is a homogroup if and only if there is an element  in
in 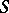 which is divisible on the left and right by any element of
which is divisible on the left and right by any element of 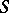 (that is,
(that is, 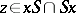 for any
for any 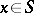 ); in this case the kernel consists of all such elements. For example, every finite commutative semi-group is a homogroup.
); in this case the kernel consists of all such elements. For example, every finite commutative semi-group is a homogroup.
If a semi-group 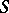 has a minimal left ideal
has a minimal left ideal 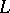 , then for any
, then for any 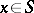 the product
the product 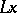 is also a minimal left ideal, moreover, every minimal left ideal can be obtained in this way. Every minimal left ideal is a left simple semi-group. In a semi-group with minimal left ideals every left ideal contains a minimal left ideal, and the union of all minimal left ideals (which are pairwise disjoint) is the kernel of the semi-group. If a semi-group
is also a minimal left ideal, moreover, every minimal left ideal can be obtained in this way. Every minimal left ideal is a left simple semi-group. In a semi-group with minimal left ideals every left ideal contains a minimal left ideal, and the union of all minimal left ideals (which are pairwise disjoint) is the kernel of the semi-group. If a semi-group 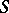 has a minimal left ideal
has a minimal left ideal 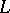 and a minimal right ideal
and a minimal right ideal 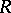 , then
, then 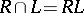 is a subgroup in
is a subgroup in 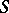 and
and 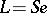 ,
, 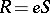 , where
, where  is the identity of this subgroup; the product
is the identity of this subgroup; the product 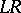 coincides with the kernel of
coincides with the kernel of 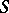 and is, in this case, a completely-simple semi-group.
and is, in this case, a completely-simple semi-group.
For semi-groups with a zero, the interest is in the consideration of non-zero ideals, and a minimal element in the corresponding partially ordered set of ideals is called a  -minimal (left, right, two-sided) ideal. The properties of
-minimal (left, right, two-sided) ideal. The properties of  -minimal ideals are in many ways similar to the properties of minimal ideals, with some natural restrictions. For example, a
-minimal ideals are in many ways similar to the properties of minimal ideals, with some natural restrictions. For example, a  -minimal two-sided ideal is not necessarily unique and need not be a
-minimal two-sided ideal is not necessarily unique and need not be a  -simple semi-group; it may be a semi-group with zero multiplication (see Nilpotent semi-group). The union of all
-simple semi-group; it may be a semi-group with zero multiplication (see Nilpotent semi-group). The union of all  -minimal left ideals (respectively,
-minimal left ideals (respectively,  -minimal right ideals) is a semi-group with zero, called its left (respectively, right) socle (by definition, the socle is equal to zero if there are no corresponding
-minimal right ideals) is a semi-group with zero, called its left (respectively, right) socle (by definition, the socle is equal to zero if there are no corresponding  -minimal ideals in the semi-group). A semi-group coincides with its left and right socles if and only if it is an
-minimal ideals in the semi-group). A semi-group coincides with its left and right socles if and only if it is an 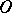 -direct union of completely-simple semi-groups and semi-groups with zero multiplication.
-direct union of completely-simple semi-groups and semi-groups with zero multiplication.
The consideration of minimal ideals and  -minimal ideals plays an essential role in the structure theory of a number of important classes of semi-groups (see, for example, Completely-simple semi-group; Regular semi-group, and also , §§ 2.5, 2.7, Chapt. 6, §§ 7.7, 8.2, 8.3; , Chapt. V).
-minimal ideals plays an essential role in the structure theory of a number of important classes of semi-groups (see, for example, Completely-simple semi-group; Regular semi-group, and also , §§ 2.5, 2.7, Chapt. 6, §§ 7.7, 8.2, 8.3; , Chapt. V).
L.N. Shevrin
Rings (like semi-groups) need not have minimal ideals (the simplest example is the ring of integers) and a minimal ideal in a ring, if it exists, need not be unique. The sum of all (left, right, two-sided) minimal ideals in a ring is called the (left, right, two-sided) socle of the ring. An Artinian ring, obviously, has a non-zero socle. The presence of minimal ideals in a primitive ring makes it close to a matrix ring in the following sense: A primitive ring with a non-zero socle is isomorphic to a dense subring of the ring of all linear transformations of some vector space over a skew-field, containing all transformations of finite rank .
V.E. Govorov
References for the above sections are given below.
References
| [1] | A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1–2 , Amer. Math. Soc. (1961–1967) |
| [2] | E.S. Lyapin, "Semigroups" , Amer. Math. Soc. (1974) (Translated from Russian) |
| [3] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) |
Comments
In commutative ring theory, and also in the theory of distributive lattices, the study of minimal prime ideals (i.e. minimal elements in the ordered set of prime ideals) plays an important part. To a large extent this is simply the order-theoretic dual of the study of maximal ideals of these structures (see Maximal ideal), but the parallel is not exact — for instance, the space of minimal prime ideals of a distributive lattice is always Hausdorff but need not be compact, whereas the space of maximal ideals is always compact but need not be Hausdorff.
References
| [a1] | M. Henriksen, M. Jerison, "The space of minimal prime ideals of a commutative ring" Trans. Amer. Math. Soc. , 115 (1965) pp. 110–130 |
| [a2] | H. Simmons, "Reticulated rings" J. Algebra , 66 (1980) pp. 169–192 |
| [a3] | S.-H. Sun, "A localic approach to minimal prime spectra" Math. Proc. Cambridge Philos. Soc. , 103 (1988) pp. 47–53 |
Minimal ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minimal_ideal&oldid=33187