Meijer transform
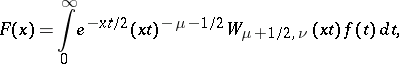 |
where  is the Whittaker function (cf. Whittaker functions). The corresponding inversion formula is
is the Whittaker function (cf. Whittaker functions). The corresponding inversion formula is
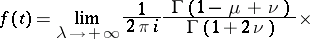 |
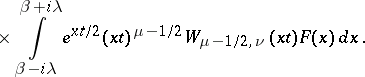 |
For  the Meijer transform becomes the Laplace transform; for
the Meijer transform becomes the Laplace transform; for  it becomes the
it becomes the  -transform
-transform
 |
where  is the Macdonald function.
is the Macdonald function.
The Varma transform
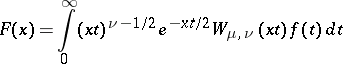 |
reduces to a Meijer transform.
The Meijer  -transform (or the Meijer–Bessel transform) is the integral transform
-transform (or the Meijer–Bessel transform) is the integral transform
 |
If the function 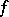 is locally integrable on
is locally integrable on  , has bounded variation in a neighbourhood of the point
, has bounded variation in a neighbourhood of the point 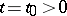 , and if the integral
, and if the integral
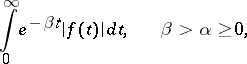 |
converges, then the following inversion formula is valid:
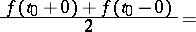 |
 |
For  the Meijer
the Meijer  -transform turns into the Laplace transform.
-transform turns into the Laplace transform.
The Meijer transform and Meijer  -transform were introduced by C.S. Meijer in [1] and, respectively, .
-transform were introduced by C.S. Meijer in [1] and, respectively, .
References
| [1] | C.S. Meijer, "Eine neue Erweiterung der Laplace Transformation I" Proc. Koninkl. Ned. Akad. Wet. , 44 (1941) pp. 727–737 |
| [2a] | C.S. Meijer, "Ueber eine neue Erweiterung der Laplace Transformation I" Proc. Koninkl. Ned. Akad. Wet. , 43 (1940) pp. 599–608 |
| [2b] | C.S. Meijer, "Ueber eine neue Erweiterung der Laplace Transformation II" Proc. Koninkl. Ned. Akad. Wet. , 43 (1940) pp. 702–711 |
| [3] | Y.A. Brychkov, A.P. Prudnikov, "Integral transforms of generalized functions" , Gordon & Breach (1989) (Translated from Russian) |
| [4] | V.A. Ditkin, A.P. Prudnikov, "Operational calculus" Progress in Math. , 1 (1968) pp. 1–75 Itogi Nauk. Mat. Anal. 1966 (1967) pp. 7–82 |
Meijer transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Meijer_transform&oldid=12567