Difference between revisions of "MediaWiki:Sidebar"
| Line 22: | Line 22: | ||
[[Bayes formula|Bayes formula]], | [[Bayes formula|Bayes formula]], | ||
has the density | has the density | ||
| − | |||
<html><table class="eq" style="width:100%;"> | <html><table class="eq" style="width:100%;"> | ||
<tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010030/a0100309.png"></td> | <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010030/a0100309.png"></td> | ||
</tr></table></html> | </tr></table></html> | ||
| + | If | ||
| + | <html><img align="absmiddle" border="0" src="images/a010/a010030/a01003010.png"></html> | ||
| + | is a | ||
| + | [[Sufficient statistic|sufficient statistic]] | ||
| + | for the family of distributions with densities | ||
| + | <html><img align="absmiddle" border="0" src="images/a010/a010030/a01003011.png">, | ||
| + | then the a posteriori distribution depends not on | ||
| + | <img align="absmiddle" border="0" src="images/a010/a010030/a01003012.png"> | ||
| + | itself, but on | ||
| + | <img align="absmiddle" border="0" src="images/a010/a010030/a01003013.png">. | ||
| + | The asymptotic behaviour of the a posteriori distribution | ||
| + | <img align="absmiddle" border="0" src="images/a010/a010030/a01003014.png"> | ||
| + | as | ||
| + | <img align="absmiddle" border="0" src="images/a010/a010030/a01003015.png">, | ||
| + | where | ||
| + | <img align="absmiddle" border="0" src="images/a010/a010030/a01003016.png"> | ||
| + | are the results of independent observations with density | ||
| + | <img align="absmiddle" border="0" src="images/a010/a010030/a01003017.png">,</html> | ||
| + | is | ||
| + |  "almost independent"  | ||
| + | of the a priori distribution of | ||
| + | <html><img align="absmiddle" border="0" src="images/a010/a010030/a01003018.png"></html>. | ||
| + | |||
| + | For the role played by a posteriori distributions | ||
| + | in the theory of statistical decisions, see | ||
| + | [[Bayesian approach|Bayesian approach]]. | ||
todo | todo | ||
Revision as of 16:37, 16 June 2010
A conditional probability distribution of a random variable, to be contrasted with its unconditional or a priori distribution.
Let
<html> be a random parameter with an a priori density
be a random parameter with an a priori density
 ,
let
,
let
 be a random result of observations and let
be a random result of observations and let
 be the conditional density of
be the conditional density of
 when
when
 ;
then the a posteriori distribution of
;
then the a posteriori distribution of
 for a given
for a given
 </html>,
according to the
Bayes formula,
has the density
</html>,
according to the
Bayes formula,
has the density
<html>
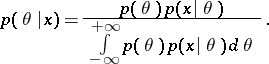 |
</html>
If
<html></html>
is a
sufficient statistic
for the family of distributions with densities
<html>
,
then the a posteriori distribution depends not on
itself, but on
.
The asymptotic behaviour of the a posteriori distribution
as
,
where
are the results of independent observations with density
,</html>
is
"almost independent"
of the a priori distribution of
<html>
</html>.
For the role played by a posteriori distributions
in the theory of statistical decisions, see
Bayesian approach.
todo
Sidebar. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sidebar&oldid=2998