Maximum-modulus principle
A theorem expressing one of the basic properties of the modulus of an analytic function. Let 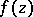 be a regular analytic, or holomorphic, function of
be a regular analytic, or holomorphic, function of  complex variables
complex variables 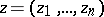 ,
, 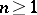 , defined on an (open) domain
, defined on an (open) domain 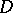 of the complex space
of the complex space 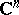 , which is not a constant,
, which is not a constant, 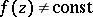 . The local formulation of the maximum-modulus principle asserts that the modulus of
. The local formulation of the maximum-modulus principle asserts that the modulus of 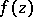 does not have a local maximum at a point
does not have a local maximum at a point 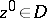 , that is, there is no neighbourhood
, that is, there is no neighbourhood 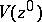 of
of 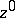 for which
for which 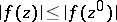 ,
, 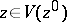 . If in addition
. If in addition 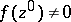 , then
, then 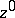 also cannot be a local minimum point of the modulus of
also cannot be a local minimum point of the modulus of 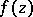 . An equivalent global formulation of the maximum-modulus principle is that, under the same conditions as above, the modulus of
. An equivalent global formulation of the maximum-modulus principle is that, under the same conditions as above, the modulus of 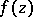 does not attain its least upper bound
does not attain its least upper bound
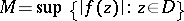 |
at any 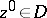 . Consequently, if
. Consequently, if 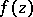 is continuous in a finite closed domain
is continuous in a finite closed domain 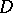 , then
, then 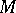 can only be attained on the boundary of
can only be attained on the boundary of 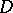 . These formulations of the maximum-modulus principle still hold when
. These formulations of the maximum-modulus principle still hold when 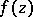 is a holomorphic function on a connected complex (analytic) manifold, in particular, on a Riemann surface or a Riemann domain (cf. Riemannian domain)
is a holomorphic function on a connected complex (analytic) manifold, in particular, on a Riemann surface or a Riemann domain (cf. Riemannian domain) 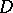 .
.
The maximum-modulus principle has generalizations in several directions. First, instead of 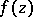 being holomorphic, it is sufficient to assume that
being holomorphic, it is sufficient to assume that 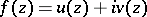 is a (complex) harmonic function. Another generalization is connected with the fact that for a holomorphic function
is a (complex) harmonic function. Another generalization is connected with the fact that for a holomorphic function  the modulus
the modulus 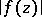 is a logarithmically-subharmonic function. If
is a logarithmically-subharmonic function. If  is a bounded holomorphic function in a finite domain
is a bounded holomorphic function in a finite domain 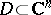 and if
and if
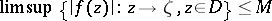 |
holds for all 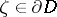 , except at some set
, except at some set  of outer capacity zero (in
of outer capacity zero (in 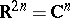 ), then
), then 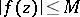 everywhere in
everywhere in 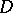 . See also Two-constants theorem; Phragmén–Lindelöf theorem.
. See also Two-constants theorem; Phragmén–Lindelöf theorem.
The maximum-modulus principle can also be generalized to holomorphic mappings. Let 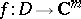 be a holomorphic mapping of an (open) domain
be a holomorphic mapping of an (open) domain 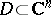 ,
, 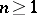 , into
, into 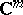 , that is,
, that is, 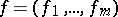 ,
, 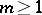 , where
, where 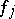 ,
, 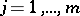 , are holomorphic functions on
, are holomorphic functions on  ,
, 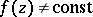 and
and 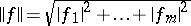 is the Euclidean norm. Then
is the Euclidean norm. Then 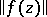 does not attain a local maximum at any
does not attain a local maximum at any 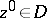 . The maximum-modulus principle is valid whenever the principle of preservation of domain is satisfied (cf. Preservation of domain, principle of).
. The maximum-modulus principle is valid whenever the principle of preservation of domain is satisfied (cf. Preservation of domain, principle of).
References
| [1] | S. Stoilov, "The theory of functions of a complex variable" , 1–2 , Moscow (1962) (In Russian; translated from Rumanian) |
| [2] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
| [3] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) |
Comments
This principle is also called the maximum principle, cf. [a2].
References
| [a1] | R.B. Burchel, "An introduction to classical complex analysis" , 1 , Acad. Press (1979) |
| [a2] | L.V. Ahlfors, "Complex analysis" , McGraw-Hill (1979) pp. 241 |
Maximum-modulus principle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximum-modulus_principle&oldid=14366