Difference between revisions of "Maximal ideal"
(Importing text file) |
m (→Comments: links) |
||
| Line 13: | Line 13: | ||
Maximal ideals also play an important role in the structure and representation theory of lattices (particularly distributive lattices). In a [[Distributive lattice|distributive lattice]], as in a commutative ring, all maximal ideals are prime; the converse implication holds in a [[Boolean algebra|Boolean algebra]], and indeed a distributive lattice in which all prime ideals are maximal is necessarily Boolean. As with rings, the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296022.png" /> of maximal ideals of a distributive lattice <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296023.png" /> can be topologized as a subspace of the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296024.png" /> of all prime ideals, and it is a compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296025.png" />-space; moreover, every compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296026.png" />-space arises in this way. A distributive lattice <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296027.png" /> is said to be normal if, given elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296028.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296029.png" />, there exist <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296030.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296031.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296032.png" />. Normal distributive lattices can be characterized as those for which every prime ideal is contained in a unique maximal ideal, or equivalently as those for which there is a continuous [[Retraction|retraction]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296033.png" /> onto <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296034.png" />; they have the property that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296035.png" /> is a Hausdorff space. For a topological space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296036.png" />, the lattice <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296037.png" /> of open subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296038.png" /> is normal if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296039.png" /> is a [[Normal space|normal space]]; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296040.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296041.png" />-space, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296042.png" /> yields a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296043.png" /> [[Compactification|compactification]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296044.png" />, which coincides with the [[Stone–Čech compactification|Stone–Čech compactification]] if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296045.png" /> is normal (see [[Wallman compactification|Wallman compactification]]). | Maximal ideals also play an important role in the structure and representation theory of lattices (particularly distributive lattices). In a [[Distributive lattice|distributive lattice]], as in a commutative ring, all maximal ideals are prime; the converse implication holds in a [[Boolean algebra|Boolean algebra]], and indeed a distributive lattice in which all prime ideals are maximal is necessarily Boolean. As with rings, the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296022.png" /> of maximal ideals of a distributive lattice <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296023.png" /> can be topologized as a subspace of the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296024.png" /> of all prime ideals, and it is a compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296025.png" />-space; moreover, every compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296026.png" />-space arises in this way. A distributive lattice <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296027.png" /> is said to be normal if, given elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296028.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296029.png" />, there exist <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296030.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296031.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296032.png" />. Normal distributive lattices can be characterized as those for which every prime ideal is contained in a unique maximal ideal, or equivalently as those for which there is a continuous [[Retraction|retraction]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296033.png" /> onto <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296034.png" />; they have the property that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296035.png" /> is a Hausdorff space. For a topological space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296036.png" />, the lattice <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296037.png" /> of open subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296038.png" /> is normal if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296039.png" /> is a [[Normal space|normal space]]; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296040.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296041.png" />-space, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296042.png" /> yields a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296043.png" /> [[Compactification|compactification]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296044.png" />, which coincides with the [[Stone–Čech compactification|Stone–Čech compactification]] if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296045.png" /> is normal (see [[Wallman compactification|Wallman compactification]]). | ||
| − | The construction of maximal ideals in arbitrary rings or lattices generally requires an appeal to Zorn's lemma (see [[ | + | The construction of maximal ideals in arbitrary rings or lattices generally requires an appeal to Zorn's lemma (see [[Axiom of choice]] or [[Zorn lemma]]), and indeed the maximal ideal theorem for many classes of rings or lattices (i.e. the assertion that every non-trivial ring or lattice in the class has a maximal ideal) has been shown to be equivalent in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062960/m06296046.png" /> set theory to the axiom of choice. This applies to the class of all (commutative) unique factorization domains, and of all Heyting algebras (see [[Brouwer lattice]]); however, for the classes of principal ideal domains, of Brouwer lattices, and of normal distributive lattices, the maximal ideal theorem is equivalent to the "[[Prime ideal theorem]]" for the corresponding class, and is strictly weaker than the axiom of choice. |
====References==== | ====References==== | ||
Revision as of 09:52, 9 October 2016
A maximal element in the partially ordered set of proper ideals of a corresponding algebraic structure. Maximal ideals play an essential role in ring theory. Every ring with identity has maximal left (also right and two-sided) ideals. The quotient module  of
of  regarded as a left (respectively, right)
regarded as a left (respectively, right)  -module relative to a left (respectively, right) maximal ideal
-module relative to a left (respectively, right) maximal ideal  is irreducible (cf. Irreducible module); a homomorphism
is irreducible (cf. Irreducible module); a homomorphism  of
of  into the field of endomorphisms of
into the field of endomorphisms of  is a representation of
is a representation of  . The kernel of all such representations, that is, the set of elements of the ring which are mapped to zero by all representations, is called the Jacobson radical of
. The kernel of all such representations, that is, the set of elements of the ring which are mapped to zero by all representations, is called the Jacobson radical of  ; it coincides with the intersection of all maximal left (also, all right) ideals.
; it coincides with the intersection of all maximal left (also, all right) ideals.
In the ring 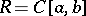 of continuous real-valued functions on a closed interval
of continuous real-valued functions on a closed interval 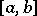 , the set of functions vanishing at some fixed point
, the set of functions vanishing at some fixed point 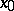 is a maximal ideal. Such ideals exhaust all maximal ideals of
is a maximal ideal. Such ideals exhaust all maximal ideals of 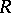 . This relation between the points of the interval and the maximal ideals has resulted in the construction of various theories for representing rings as rings of functions on a topological space.
. This relation between the points of the interval and the maximal ideals has resulted in the construction of various theories for representing rings as rings of functions on a topological space.
The Zariski topology on the set of prime ideals (cf. Prime ideal) 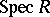 of a ring
of a ring 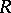 has weak separation properties (that is, there are non-closed points). A similar topology in the non-commutative case can be introduced on the set
has weak separation properties (that is, there are non-closed points). A similar topology in the non-commutative case can be introduced on the set 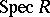 of primitive ideals (cf. Primitive ideal), which are the annihilators of irreducible
of primitive ideals (cf. Primitive ideal), which are the annihilators of irreducible 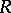 -modules. The set of maximal ideals, and in the non-commutative case, of maximal primitive ideals, forms a subspace
-modules. The set of maximal ideals, and in the non-commutative case, of maximal primitive ideals, forms a subspace 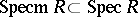 which satisfies the
which satisfies the  -separation axiom.
-separation axiom.
References
| [1] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) |
Comments
Maximal ideals also play an important role in the structure and representation theory of lattices (particularly distributive lattices). In a distributive lattice, as in a commutative ring, all maximal ideals are prime; the converse implication holds in a Boolean algebra, and indeed a distributive lattice in which all prime ideals are maximal is necessarily Boolean. As with rings, the set 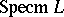 of maximal ideals of a distributive lattice
of maximal ideals of a distributive lattice  can be topologized as a subspace of the space
can be topologized as a subspace of the space 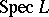 of all prime ideals, and it is a compact
of all prime ideals, and it is a compact  -space; moreover, every compact
-space; moreover, every compact  -space arises in this way. A distributive lattice
-space arises in this way. A distributive lattice 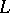 is said to be normal if, given elements
is said to be normal if, given elements 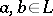 with
with 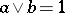 , there exist
, there exist  with
with 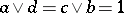 and
and 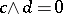 . Normal distributive lattices can be characterized as those for which every prime ideal is contained in a unique maximal ideal, or equivalently as those for which there is a continuous retraction of
. Normal distributive lattices can be characterized as those for which every prime ideal is contained in a unique maximal ideal, or equivalently as those for which there is a continuous retraction of  onto
onto 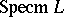 ; they have the property that
; they have the property that 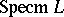 is a Hausdorff space. For a topological space
is a Hausdorff space. For a topological space  , the lattice
, the lattice 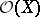 of open subsets of
of open subsets of 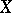 is normal if and only if
is normal if and only if 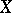 is a normal space; if
is a normal space; if 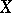 is a
is a 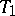 -space, then
-space, then 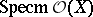 yields a
yields a  compactification of
compactification of 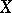 , which coincides with the Stone–Čech compactification if
, which coincides with the Stone–Čech compactification if 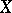 is normal (see Wallman compactification).
is normal (see Wallman compactification).
The construction of maximal ideals in arbitrary rings or lattices generally requires an appeal to Zorn's lemma (see Axiom of choice or Zorn lemma), and indeed the maximal ideal theorem for many classes of rings or lattices (i.e. the assertion that every non-trivial ring or lattice in the class has a maximal ideal) has been shown to be equivalent in 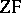 set theory to the axiom of choice. This applies to the class of all (commutative) unique factorization domains, and of all Heyting algebras (see Brouwer lattice); however, for the classes of principal ideal domains, of Brouwer lattices, and of normal distributive lattices, the maximal ideal theorem is equivalent to the "Prime ideal theorem" for the corresponding class, and is strictly weaker than the axiom of choice.
set theory to the axiom of choice. This applies to the class of all (commutative) unique factorization domains, and of all Heyting algebras (see Brouwer lattice); however, for the classes of principal ideal domains, of Brouwer lattices, and of normal distributive lattices, the maximal ideal theorem is equivalent to the "Prime ideal theorem" for the corresponding class, and is strictly weaker than the axiom of choice.
References
| [a1] | P.T. Johnstone, "Stone spaces" , Cambridge Univ. Press (1983) |
In the theory of semi-groups (cf. Semi-group) maximal ideals play a lesser role than minimal ideals (cf. Minimal ideal). If 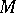 is a maximal two-sided ideal of a semi-group
is a maximal two-sided ideal of a semi-group 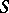 , then either
, then either 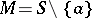 , where
, where  is some indecomposable element of
is some indecomposable element of  (that is,
(that is, 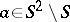 ), or
), or 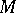 is a prime ideal (that is, for any two ideals
is a prime ideal (that is, for any two ideals  and
and 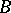 ,
,  implies
implies 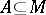 or
or 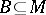 ). This implies that every maximal two-sided ideal in
). This implies that every maximal two-sided ideal in 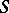 is prime if and only if
is prime if and only if 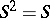 . In a semi-group
. In a semi-group 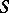 with a maximal two-sided ideal a prime ideal
with a maximal two-sided ideal a prime ideal  is maximal if (and, obviously, only if)
is maximal if (and, obviously, only if) 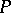 contains the intersection
contains the intersection 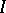 of all maximal two-sided ideals of
of all maximal two-sided ideals of 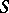 . The Rees quotient semi-group
. The Rees quotient semi-group  is an
is an 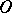 -direct union of semi-groups each of which is either
-direct union of semi-groups each of which is either  -simple or two-element nilpotent.
-simple or two-element nilpotent.
Sometimes a semi-group 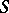 with proper left ideals may have a largest such ideal
with proper left ideals may have a largest such ideal 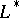 (that is, containing all other proper left ideals). This, for example, is the case when
(that is, containing all other proper left ideals). This, for example, is the case when 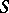 has a right identity. In that case, if
has a right identity. In that case, if 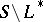 is not a singleton, then it is a sub-semi-group. In a periodic semi-group
is not a singleton, then it is a sub-semi-group. In a periodic semi-group 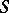 the existence of
the existence of 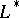 implies that
implies that 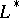 is a (largest proper) two-sided ideal. Another example is given by subgroups with separating group part (see Invertible element) which is not a group.
is a (largest proper) two-sided ideal. Another example is given by subgroups with separating group part (see Invertible element) which is not a group.
References
| [1a] | S. Schwarz, "On maximal ideals in the theory of semigroups I" Czechoslovak. Math. J. , 3 (1953) pp. 139–153 (In Russian) (English abstract) |
| [1b] | S. Schwarz, "On maximal ideals in the theory of semigroups II" Czechoslovak. Math. J. , 4 (1953) pp. 365–383 (In Russian) (English abstract) |
| [2] | S. Schwarz, "Prime ideals and maximal ideals in semigroups" Czechoslovak. Math. J. , 19 (1969) pp. 72–79 |
| [3] | P.A. Grillet, "Intersections of maximal ideals in semigroups" Amer. Math. Monthly , 76 (1969) pp. 503–509 |
L.N. Shevrin
Maximal ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximal_ideal&oldid=17927