Matrix ring
full matrix ring
The ring of all square matrices of a fixed order over a ring  . The ring of
. The ring of  -dimensional matrices over
-dimensional matrices over  is denoted by
is denoted by  or
or  . Throughout this article
. Throughout this article  is an associative ring with identity (cf. Associative rings and algebras).
is an associative ring with identity (cf. Associative rings and algebras).
The ring  is isomorphic to the ring
is isomorphic to the ring  of all endomorphisms of the free right
of all endomorphisms of the free right  -module
-module 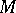 , possessing a basis with
, possessing a basis with  elements. The matrix
elements. The matrix  is the identity in
is the identity in 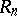 . An associative ring
. An associative ring 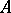 with identity 1 is isomorphic to
with identity 1 is isomorphic to 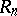 if and only if there is in
if and only if there is in 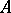 a set of
a set of 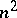 elements
elements 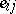 ,
, 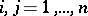 , subject to the following conditions:
, subject to the following conditions:
1) 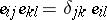 ,
, 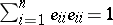 ;
;
2) the centralizer of the set of elements  in
in  is isomorphic to
is isomorphic to 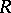 .
.
The centre of 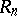 coincides with
coincides with 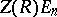 , where
, where 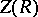 is the centre of
is the centre of 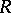 ; for
; for 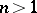 the ring
the ring 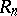 is non-commutative.
is non-commutative.
The multiplicative group of the ring 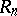 (the group of all invertible elements), called the general linear group, is denoted by
(the group of all invertible elements), called the general linear group, is denoted by  . A matrix from
. A matrix from  is invertible in
is invertible in 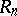 if and only if its columns form a basis of the free right module of all
if and only if its columns form a basis of the free right module of all  -dimensional matrices over
-dimensional matrices over 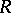 . If
. If 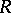 is commutative, then the invertibility of a matrix
is commutative, then the invertibility of a matrix  in
in 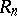 is equivalent to the invertibility of its determinant,
is equivalent to the invertibility of its determinant, 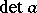 , in
, in 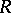 . The equality
. The equality 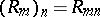 holds.
holds.
The ring 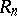 is simple if and only if
is simple if and only if  is simple, for the two-sided ideals in
is simple, for the two-sided ideals in  are of the form
are of the form 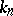 , where
, where 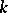 is a two-sided ideal in
is a two-sided ideal in  . An Artinian ring is simple if and only if it is isomorphic to a matrix ring over a skew-field (the Wedderburn–Artin theorem). If
. An Artinian ring is simple if and only if it is isomorphic to a matrix ring over a skew-field (the Wedderburn–Artin theorem). If 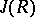 denotes the Jacobson radical of the ring
denotes the Jacobson radical of the ring 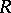 , then
, then  . Consequently, every matrix ring over a semi-simple ring
. Consequently, every matrix ring over a semi-simple ring 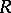 is semi-simple. If
is semi-simple. If 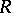 is regular (i.e. if for every
is regular (i.e. if for every 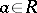 there is a
there is a 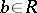 such that
such that 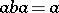 ), then so is
), then so is 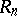 . If
. If 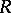 is a ring with an invariant basis number, i.e. the number of elements in a basis of each free
is a ring with an invariant basis number, i.e. the number of elements in a basis of each free 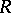 -module does not depend of the choice of the basis, then
-module does not depend of the choice of the basis, then 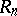 also has this property. The rings
also has this property. The rings  and
and 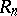 are equivalent in the sense of Morita (see Morita equivalence): The category of
are equivalent in the sense of Morita (see Morita equivalence): The category of 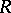 -modules is equivalent to the category of
-modules is equivalent to the category of 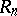 -modules. However, the fact that projective
-modules. However, the fact that projective 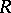 -modules are free does not necessarily entail that projective
-modules are free does not necessarily entail that projective 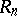 -modules are free too. For instance, if
-modules are free too. For instance, if 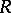 is a field and
is a field and 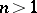 , then there exist finitely-generated projective
, then there exist finitely-generated projective 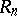 -modules which are not free.
-modules which are not free.
References
| [1] | C. Faith, "Algebra: rings, modules, and categories" , 1 , Springer (1973) |
| [2] | J. Lambek, "Lectures on rings and modules" , Blaisdell (1966) |
| [3] | L.A. Bokut', "Associative rings" , 1 , Novosibirsk (1977) (In Russian) |
Comments
References
| [a1] | P.M. Cohn, "Algebra" , 1–2 , Wiley (1974–1977) |
Matrix ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Matrix_ring&oldid=15509