Matrix game
A two-person zero-sum game in which each player possesses only a finite number of pure strategies. If player I possesses 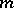 strategies and player II possesses
strategies and player II possesses  strategies, then the matrix game can be given by an
strategies, then the matrix game can be given by an  -matrix
-matrix  , where
, where  ,
,  ,
,  , is the payoff of player I if (s)he chooses strategy
, is the payoff of player I if (s)he chooses strategy  while player II chooses strategy
while player II chooses strategy  . According to the general optimality principle in two-person zero-sum games (see also Minimax principle), player I tends to choose a strategy
. According to the general optimality principle in two-person zero-sum games (see also Minimax principle), player I tends to choose a strategy  on which
on which
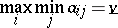 |
is attained, whereas player II tends to choose a strategy 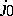 on which
on which
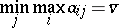 |
is attained. If  , then the pair
, then the pair 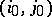 is called a saddle point (cf. Saddle point in game theory) of the game; the number
is called a saddle point (cf. Saddle point in game theory) of the game; the number 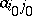 is called the value of the game, and the strategies
is called the value of the game, and the strategies 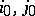 are optimal pure strategies. If
are optimal pure strategies. If 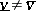 (i.e. a pure strategy solution does not exist), then always
(i.e. a pure strategy solution does not exist), then always 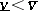 . In this case one must seek the optimal strategies of the players among their mixed strategies (cf. Strategy (in game theory)). Let
. In this case one must seek the optimal strategies of the players among their mixed strategies (cf. Strategy (in game theory)). Let  (respectively,
(respectively,  ) be the set of mixed strategies of player I (respectively, player II). Then players I and II will tend to choose the strategies
) be the set of mixed strategies of player I (respectively, player II). Then players I and II will tend to choose the strategies 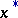 and
and 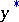 on which
on which
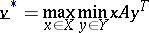 |
and
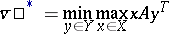 |
are attained, respectively (the superscript 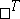 denotes transposition). The main theorem in the theory of matrix games (von Neumann's minimax theorem) asserts that
denotes transposition). The main theorem in the theory of matrix games (von Neumann's minimax theorem) asserts that 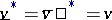 , i.e. for every matrix game there are optimal mixed strategies
, i.e. for every matrix game there are optimal mixed strategies 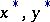 and a value
and a value  of the game.
of the game.
For the numerical solution of matrix games (i.e. for finding optimal strategies and the value of the game) one most frequently uses the fact that the problem of solving a matrix game can be reduced to a linear programming problem. A less efficient approach is the Brown–Robinson iterative method, which amounts to "playing" fictitiously the matrix game so that at each step the players choose the best pure strategies under an "accumulated" mixed strategy of the opponent. Matrix games in which one of the players has only two strategies are readily solved using graphical methods.
Matrix games serve as mathematical models of many of the simplest conflict situations in the areas of economics, mathematical statistics, war science, and biology. In applications, the role of one of the players is sometimes assigned to "nature" , by which one understands the totality of external circumstances which are unknown to the decision maker (the other player).
References
| [1] | J.M. Dresher, "Games of strategy: theory and practice" , Prentice-Hall (1961) |
| [2] | J. von Neumann, O. Morgenstern, "Theory of games and economic behavior" , Princeton Univ. Press (1947) |
| [3] | H.G. Owen, "Game theory" , Saunders (1968) |
| [4] | N.N. Vorob'ev, "Game theory. Lectures for economists and system scientists" , Springer (1977) (Translated from Russian) |
Comments
The theory of matrix games is divided into zero-sum and non-zero-sum games. Two-person non-zero-sum matrix games are usually referred to as bimatrix games, cf. Bimatrix game.
References
| [a1] | S. Karlin, "Matrix games, programming and mathematical economics" , 1–2 , Addison-Wesley (1959) |
Matrix game. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Matrix_game&oldid=15889