Difference between revisions of "Masser-Philippon/Lazard-Mora example"
From Encyclopedia of Mathematics
Ulf Rehmann (talk | contribs) m (moved Masser–Philippon/Lazard–Mora example to Masser-Philippon/Lazard-Mora example: ascii title) |
m (Automatically changed introduction) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 10 formulas, 6 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|part}} | ||
''Lazard–Mora/Masser–Philippon example, Lazard–Mora example, Masser–Philippon example'' | ''Lazard–Mora/Masser–Philippon example, Lazard–Mora example, Masser–Philippon example'' | ||
An extremal family for the degrees in the Hilbert Nullstellensatz (cf. [[Hilbert theorem|Hilbert theorem]]) is given by the following example, ascribed variously to D.W. Masser and P. Philippon and to D. Lazard and T. Mora: | An extremal family for the degrees in the Hilbert Nullstellensatz (cf. [[Hilbert theorem|Hilbert theorem]]) is given by the following example, ascribed variously to D.W. Masser and P. Philippon and to D. Lazard and T. Mora: | ||
| − | + | \begin{equation*} f _ { 1 } : = x _ { 1 } ^ { d }, \end{equation*} | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130060/m1300602.png"/></td> </tr></table> |
| − | The | + | The $f_i$ are readily seen to have no common zeros. If $a _ { 1 } , \dots , a _ { m }$ are polynomials such that |
| − | + | \begin{equation*} a _ { 1 } f _ { 1 } + \ldots + a _ { m } f _ { m } = 1, \end{equation*} | |
by evaluation on the rational curve | by evaluation on the rational curve | ||
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130060/m1300606.png"/></td> </tr></table> |
| − | it is easy to see that | + | it is easy to see that $\operatorname{deg}_{x_m} a _ { 1 } \geq d ^ { m - 1 } ( d - 1 )$. This lower bound of order $d ^ { m }$ for the degrees of the coefficients for the Nullstellensatz is much better than the doubly exponential lower bound for the general ideal membership problem given in [[#References|[a2]]]. Variants of the example, cf. [[#References|[a3]]], show that the terms in the [[Liouville–Łojasiewicz inequality|Liouville–Łojasiewicz inequality]] are nearly optimal, with the presumed exception depending solely on the degree. |
Another family of extremal examples for the Nullstellensatz is given in [[#References|[a1]]]. | Another family of extremal examples for the Nullstellensatz is given in [[#References|[a1]]]. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> J. Kollár, "Sharp effective Nullstellensatz" ''J. Amer. Math. Soc.'' , '''1''' (1988) pp. 963–975</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> E.W. Mayr, A.R. Meyer, "The complexity of the word problems in commutative semigroups and polynlomial ideals" ''Adv. Math.'' , '''46''' (1982) pp. 305–329</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> W.D. Brownawell, "Local diophantine Nullstellen equalities" ''J. Amer. Math. Soc.'' , '''1''' (1988) pp. 311–322</td></tr></table> |
Latest revision as of 17:45, 1 July 2020
Lazard–Mora/Masser–Philippon example, Lazard–Mora example, Masser–Philippon example
An extremal family for the degrees in the Hilbert Nullstellensatz (cf. Hilbert theorem) is given by the following example, ascribed variously to D.W. Masser and P. Philippon and to D. Lazard and T. Mora:
\begin{equation*} f _ { 1 } : = x _ { 1 } ^ { d }, \end{equation*}
 |
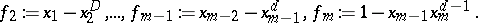The $f_i$ are readily seen to have no common zeros. If $a _ { 1 } , \dots , a _ { m }$ are polynomials such that
\begin{equation*} a _ { 1 } f _ { 1 } + \ldots + a _ { m } f _ { m } = 1, \end{equation*}
by evaluation on the rational curve
 |
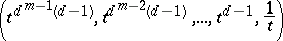it is easy to see that $\operatorname{deg}_{x_m} a _ { 1 } \geq d ^ { m - 1 } ( d - 1 )$. This lower bound of order $d ^ { m }$ for the degrees of the coefficients for the Nullstellensatz is much better than the doubly exponential lower bound for the general ideal membership problem given in [a2]. Variants of the example, cf. [a3], show that the terms in the Liouville–Łojasiewicz inequality are nearly optimal, with the presumed exception depending solely on the degree.
Another family of extremal examples for the Nullstellensatz is given in [a1].
References
| [a1] | J. Kollár, "Sharp effective Nullstellensatz" J. Amer. Math. Soc. , 1 (1988) pp. 963–975 |
| [a2] | E.W. Mayr, A.R. Meyer, "The complexity of the word problems in commutative semigroups and polynlomial ideals" Adv. Math. , 46 (1982) pp. 305–329 |
| [a3] | W.D. Brownawell, "Local diophantine Nullstellen equalities" J. Amer. Math. Soc. , 1 (1988) pp. 311–322 |
How to Cite This Entry:
Masser-Philippon/Lazard-Mora example. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Masser-Philippon/Lazard-Mora_example&oldid=22793
Masser-Philippon/Lazard-Mora example. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Masser-Philippon/Lazard-Mora_example&oldid=22793
This article was adapted from an original article by W. Dale Brownawell (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article