Logarithmic branch point
branch point of infinite order
A special form of a branch point  of an analytic function
of an analytic function 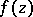 of one complex variable
of one complex variable  , when for no finite number of successive circuits in the same direction about
, when for no finite number of successive circuits in the same direction about  the analytic continuation of some element of
the analytic continuation of some element of 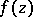 returns to the original element. More precisely, an isolated singular point
returns to the original element. More precisely, an isolated singular point  is called a logarithmic branch point for
is called a logarithmic branch point for 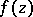 if there exist: 1) an annulus
if there exist: 1) an annulus 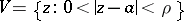 in which
in which 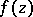 can be analytically continued along any path; and 2) a point
can be analytically continued along any path; and 2) a point 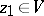 and an element of
and an element of 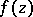 in the form of a power series
in the form of a power series 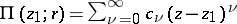 with centre
with centre 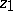 and radius of convergence
and radius of convergence 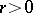 , the analytic continuation of which along the circle
, the analytic continuation of which along the circle  , taken arbitrarily many times in the same direction, never returns to the original element
, taken arbitrarily many times in the same direction, never returns to the original element 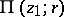 . In the case of a logarithmic branch point at infinity,
. In the case of a logarithmic branch point at infinity, 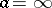 , instead of
, instead of 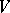 one must consider a neighbourhood
one must consider a neighbourhood 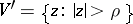 . Logarithmic branch points belong to the class of transcendental branch points (cf. Transcendental branch point). The behaviour of the Riemann surface
. Logarithmic branch points belong to the class of transcendental branch points (cf. Transcendental branch point). The behaviour of the Riemann surface 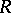 of a function
of a function 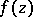 in the presence of a logarithmic branch point
in the presence of a logarithmic branch point  is characterized by the fact that infinitely many sheets of the same branch of
is characterized by the fact that infinitely many sheets of the same branch of 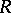 are joined over
are joined over  ; this branch is defined in
; this branch is defined in 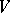 or
or 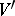 by the elements
by the elements 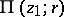 .
.
See also Singular point of an analytic function.
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 2 , Chelsea (1977) pp. Chapt. 8 (Translated from Russian) |
Comments
The function 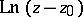 has a logarithmic branch point at
has a logarithmic branch point at 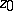 , where
, where 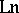 is the (multiple-valued) logarithmic function of a complex variable.
is the (multiple-valued) logarithmic function of a complex variable.
References
| [a1] | L.V. Ahlfors, "Complex analysis" , McGraw-Hill (1979) pp. Chapt. 8 |
Logarithmic branch point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Logarithmic_branch_point&oldid=11411