Liouville normal form
From Encyclopedia of Mathematics
A way of writting a second-order ordinary linear differential equation
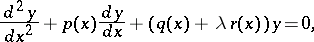 | (1) |
in the form
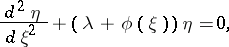 | (2) |
where 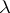 is parameter. If
is parameter. If 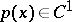 ,
, 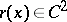 and
and 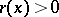 , then equation (1) reduces to the Liouville normal form (2) by means of the substitution
, then equation (1) reduces to the Liouville normal form (2) by means of the substitution
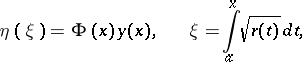 |
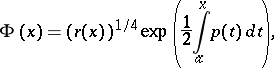 |
which is called the Liouville transformation (introduced in [1]). The Liouville normal form plays an important role in the investigation of the asymptotic behaviour of solutions of (1) for large values of the parameter  or the argument, and in the investigation of the asymptotics of eigen functions and eigen values of the Sturm–Liouville problem (see [3]).
or the argument, and in the investigation of the asymptotics of eigen functions and eigen values of the Sturm–Liouville problem (see [3]).
References
| [1] | J. Liouville, J. Math. Pures Appl. , 2 (1837) pp. 16–35 |
| [2] | E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1947) |
| [3] | E.C. Titchmarsh, "Eigenfunction expansions associated with second-order differential equations" , 1–2 , Clarendon Press (1946–1948) |
Comments
References
| [a1] | E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956) |
How to Cite This Entry:
Liouville normal form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Liouville_normal_form&oldid=27240
Liouville normal form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Liouville_normal_form&oldid=27240
This article was adapted from an original article by M.V. Fedoryuk (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article