Linear algebraic equation
An algebraic equation of the first degree in all unknowns, that is, an equation of the form
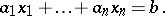 |
Every system of linear algebraic equations can be written in the form
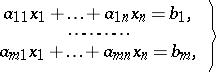 | (1) |
where 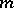 and
and  are natural numbers; the
are natural numbers; the 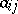 (
(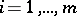 ;
; 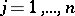 ) are called the coefficients at the unknowns and are given; the
) are called the coefficients at the unknowns and are given; the 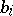 (
(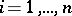 ) are called the free terms and are also given; the
) are called the free terms and are also given; the 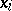 (
(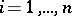 ) are called the unknowns and need to be found. A solution of the system of linear algebraic equations (1) is a set of values
) are called the unknowns and need to be found. A solution of the system of linear algebraic equations (1) is a set of values  such that each equation of the system becomes an identity when the
such that each equation of the system becomes an identity when the 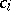 are substituted for the corresponding unknowns. For applications the most important case is that in which the coefficients at the unknowns, the free terms and the values of the unknowns are numbers (complex, real or integers), but one can also consider the case when they belong to an arbitrary field
are substituted for the corresponding unknowns. For applications the most important case is that in which the coefficients at the unknowns, the free terms and the values of the unknowns are numbers (complex, real or integers), but one can also consider the case when they belong to an arbitrary field 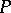 .
.
According to the number of solutions, systems of linear algebraic equations split into the following types:
a compatible system is a system of linear equations having at least one solution;
an incompatible (or contradictory) system is a system having no solution;
a determinate system is a system having a unique solution;
an indeterminate system is a system having more than one solution.
If one considers solutions of a system with values of the unknowns in a given number field (or in an arbitrary infinite field), then every indeterminate system of linear equations has infinitely many solutions. In contrast to equations of degree exceeding one, the type of a system of linear algebraic equations does not change when the given field 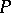 is extended. Thus, under a field extension an incompatible system cannot become compatible, and a determinate system cannot become indeterminate. However, the set of solutions of an indeterminate system is increased by this.
is extended. Thus, under a field extension an incompatible system cannot become compatible, and a determinate system cannot become indeterminate. However, the set of solutions of an indeterminate system is increased by this.
The simplest way of determining the type of the system (1) and calculating its solutions is given by the Gauss method of eliminating the unknowns. In the case 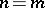 the system (1) is determinate if and only if the determinant formed by the coefficients of the unknowns is non-zero. In this case the unique solution of the system is found by Cramer's formulas (see Cramer rule).
the system (1) is determinate if and only if the determinant formed by the coefficients of the unknowns is non-zero. In this case the unique solution of the system is found by Cramer's formulas (see Cramer rule).
To solve a system of linear equations whose coefficients contain parameters, instead of Gauss' method it is more convenient to use the general theory of linear equations, associated with the rank of a matrix. The rank of a matrix can be defined as the maximal number of linearly independent rows or columns. By the theorem on the rank of a matrix, the rank of the system of rows of a matrix is equal to the rank of the system of columns and is also equal to the highest order of the non-zero minors of the matrix (cf. Minor). With the system of linear equations (1) one associates two matrices: the matrix
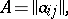 |
formed by the coefficients of the unknowns, and the extended matrix
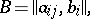 |
obtained from 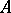 by adjoining the column of free terms. A criterion for the system (1) to be compatible is given by the Kronecker–Capelli theorem: A system of linear equations (1) is compatible if and only if the rank of
by adjoining the column of free terms. A criterion for the system (1) to be compatible is given by the Kronecker–Capelli theorem: A system of linear equations (1) is compatible if and only if the rank of 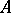 is equal to the rank of
is equal to the rank of 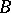 .
.
A system of linear equations (1) has a unique solution if and only if the rank of 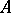 is equal to the rank of
is equal to the rank of 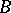 and equal to
and equal to  .
.
The unknowns of a compatible system of linear equation subdivide into principal and free unknowns. For any values of the free unknowns there are uniquely determined values of the principal unknowns, which together give a solution of the given system. The subdivision into principal and free unknowns is usually not unique. Namely, if the rank of 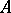 is equal to the rank of
is equal to the rank of 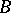 and equal to
and equal to  , then any
, then any  unknowns from the coefficients of which one can form a determinant
unknowns from the coefficients of which one can form a determinant 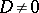 can be regarded as principal, and the others as free. In this case the determinant
can be regarded as principal, and the others as free. In this case the determinant 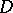 is said to be a principal (or basic) minor of the system. It can be found by the bordering method, beginning with minors of lowest orders. It is also not always defined uniquely. In the calculation of solutions one needs to take only the
is said to be a principal (or basic) minor of the system. It can be found by the bordering method, beginning with minors of lowest orders. It is also not always defined uniquely. In the calculation of solutions one needs to take only the  equations containing the principal minor
equations containing the principal minor 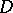 and to express the principal unknowns in general form (for example, by using Cramer's formulas) in terms of the free unknowns. These expressions are called the general solution. The free unknowns play the role of free parameters in it. Giving any values to them, one finds the values of principal unknowns that give a solution of the system with the chosen values of free unknowns. Any solution of a compatible system can be obtained in this way for suitable values of the free unknowns. If all coefficients at the unknowns and the free terms belong to a field
and to express the principal unknowns in general form (for example, by using Cramer's formulas) in terms of the free unknowns. These expressions are called the general solution. The free unknowns play the role of free parameters in it. Giving any values to them, one finds the values of principal unknowns that give a solution of the system with the chosen values of free unknowns. Any solution of a compatible system can be obtained in this way for suitable values of the free unknowns. If all coefficients at the unknowns and the free terms belong to a field 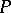 , then by choosing for the free unknowns values from the same field
, then by choosing for the free unknowns values from the same field 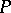 one obtains a solution with the values of all unknowns from the same field
one obtains a solution with the values of all unknowns from the same field 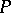 . For
. For 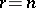 all unknowns are principal and there is no general solution.
all unknowns are principal and there is no general solution.
The system of linear equations
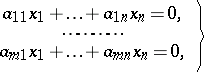 | (2) |
obtained from (1) by replacing the free terms by zeros, is called the homogeneous system of linear equations corresponding to (1). The system (2) is always compatible (since the zero solution satisfies it). For it to have a non-zero solution it is necessary and sufficient that the rank of its matrix 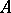 should be less than the number of unknowns
should be less than the number of unknowns  . In particular, for
. In particular, for  a square homogeneous system of linear algebraic equations has a non-zero solution if and only if its determinant is equal to zero.
a square homogeneous system of linear algebraic equations has a non-zero solution if and only if its determinant is equal to zero.
The solutions of a compatible system of linear algebraic equations (1) and the corresponding homogeneous system (2) are connected as follows: The sum of a solution of (1) and a solution of (2) is a solution of (1); the difference between two solutions of (1) is a solution of (2). All solutions of (1) can be obtained by adding to every solution of (2) the same particular solution of (1).
Geometric interpretation of solutions of a system of linear equations.
Any row of  elements of a field
elements of a field 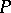 can be regarded as the row of coordinates of a vector
can be regarded as the row of coordinates of a vector  of an
of an  -dimensional vector space
-dimensional vector space 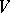 over
over 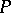 in some fixed basis. For brevity the vector
in some fixed basis. For brevity the vector  is identified with the row of its coordinates. All solutions of the homogeneous system (2) form a subspace
is identified with the row of its coordinates. All solutions of the homogeneous system (2) form a subspace 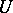 of
of 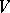 . Its dimension is equal to
. Its dimension is equal to 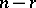 , where
, where  is the number of unknowns and
is the number of unknowns and  is the rank of the matrix
is the rank of the matrix 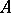 of the system. If
of the system. If 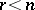 , the subspace
, the subspace 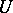 is non-zero and a basis of it is also called a fundamental system of solutions of the system of linear equations (2). Conversely, for every subspace
is non-zero and a basis of it is also called a fundamental system of solutions of the system of linear equations (2). Conversely, for every subspace 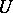 of
of  there is a homogeneous system of linear equations whose solutions form
there is a homogeneous system of linear equations whose solutions form 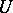 . The set of vectors
. The set of vectors 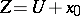 obtained by adding to each vector of
obtained by adding to each vector of 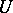 the same vector
the same vector 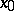 is called a linear variety (or linear manifold) of
is called a linear variety (or linear manifold) of 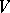 . In case
. In case 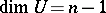 the phrase hyperplane is also used. All solutions of a compatible system of linear equations (1) form a linear variety
the phrase hyperplane is also used. All solutions of a compatible system of linear equations (1) form a linear variety 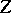 ; conversely, for any linear variety
; conversely, for any linear variety  there is a compatible system whose solutions form the given variety (see [3]).
there is a compatible system whose solutions form the given variety (see [3]).
Solution of systems of linear equations in integers.
Suppose a system of equations (1) is given in which all 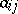 and
and 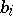 are integers. Let
are integers. Let 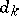 ,
, 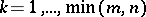 , denote the greatest common divisor of all minors of order
, denote the greatest common divisor of all minors of order 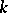 of the matrix
of the matrix 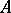 formed by the coefficients of the unknowns, and let
formed by the coefficients of the unknowns, and let 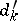 ,
, 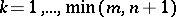 , denote the analogous number for the extended matrix
, denote the analogous number for the extended matrix 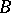 . If all minors of order
. If all minors of order 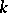 in
in 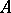 (or
(or 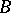 ) are zero, one puts
) are zero, one puts 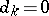 (respectively,
(respectively, 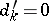 ). For a system of linear equations in integers (1) to have an integer solution it is necessary and sufficient that
). For a system of linear equations in integers (1) to have an integer solution it is necessary and sufficient that 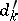 is divisible by
is divisible by 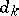 ,
, 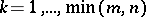 , and that
, and that 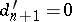 for
for 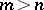 .
.
To state a method of calculating all integer solutions of a system of linear equations one introduces the so-called elementary transformations of integer matrices: 1) adding to the 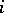 -th row the
-th row the 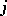 -th row
-th row 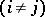 multiplied by an integer
multiplied by an integer  ; 2) multiplying the
; 2) multiplying the  -th row by
-th row by 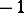 ; 3) interchanging the
; 3) interchanging the 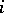 -th and
-th and 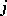 -th rows; and similar transformations of columns. Under elementary transformations of the rows the system (1) is transformed into an equivalent system, and hence the set of integer solutions is unchanged. Among the elementary transformations of the columns of the matrix
-th rows; and similar transformations of columns. Under elementary transformations of the rows the system (1) is transformed into an equivalent system, and hence the set of integer solutions is unchanged. Among the elementary transformations of the columns of the matrix 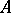 formed by the coefficients of the unknowns, the following transformations of unknowns occur: If
formed by the coefficients of the unknowns, the following transformations of unknowns occur: If  are new unknowns, then under a transformation 1),
are new unknowns, then under a transformation 1),
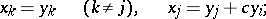 |
under a transformation 2),
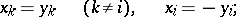 |
under a transformation 3),
 |
Under such transformations of the unknowns, integer solutions correspond to integer solutions.
A system (1) for which the rank of 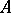 is equal to the rank of
is equal to the rank of 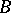 and equal to
and equal to  can be reduced, by elementary transformations of the rows of
can be reduced, by elementary transformations of the rows of 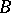 and the columns of
and the columns of 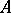 , and also by discarding zero equations, to the canonical form
, and also by discarding zero equations, to the canonical form
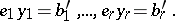 |
The numbers 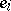 satisfy the following additional conditions:
satisfy the following additional conditions:
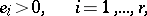 |
and
 |
These additional conditions are not essential for the problem of solving the system in integers.
For integer solutions of
to exist it is necessary and sufficient that the numbers
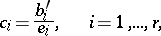 |
be integers. The unknowns 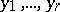 are uniquely determined, and for
are uniquely determined, and for 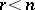 the unknowns
the unknowns 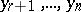 can take any integer values.
can take any integer values.
To calculate the solutions of the original system (1) one must apply all transformations of columns of 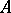 in the same order to the unit matrix
in the same order to the unit matrix 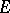 of order
of order  . The resulting integer matrix
. The resulting integer matrix 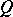 gives the relation between the old and new unknowns:
gives the relation between the old and new unknowns:
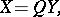 |
where
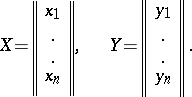 |
One must then put  ,
, 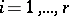 , and for
, and for 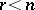 one can assign any integer values to the unknowns
one can assign any integer values to the unknowns 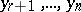 , which play the role of parameters.
, which play the role of parameters.
This method of solving (1) over the ring of integers can be generalized to any Euclidean ring or principal ideal ring.
The investigation of integer solutions and systems in the general case is the subject of the theory of Diophantine equations.
References
| [1] | A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian) |
| [2] | A.I. Kostrikin, "Introduction to algebra" , Springer (1982) (Translated from Russian) |
| [3] | A.P. Mishina, I.V. Proskuryakov, "Higher algebra. Linear algebra, polynomials, general algebra" , Pergamon (1965) (Translated from Russian) |
Comments
References
| [a1] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French) |
| [a2] | S. Lang, "Algebra" , Addison-Wesley (1984) |
| [a3] | S. Lang, "Linear algebra" , Addison-Wesley (1966) |
| [a4] | S. Lang, "Introduction to linear algebra" , Addison-Wesley (1970) |
Linear algebraic equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_algebraic_equation&oldid=16383