Lindelöf summation method
A semi-continuous method for summing series of numbers and functions (cf. Summation methods), defined by the system of functions
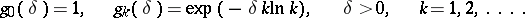 |
The series
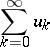 |
is summable by the Lindelöf summation method to the sum  if
if
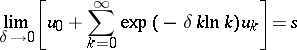 |
and the series under the limit sign converges. The method was introduced by E. Lindelöf [1] for the summation of power series.
The Lindelöf summation method is regular (see Regular summation methods) and is used as a tool for the analytic continuation of functions. If  is the principal branch of an analytic function, regular at the origin and representable by a series
is the principal branch of an analytic function, regular at the origin and representable by a series
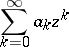 |
for small  , then this series is summable by the Lindelöf summation method to
, then this series is summable by the Lindelöf summation method to  in the whole star of the function
in the whole star of the function  (cf. Star of a function element), and it is uniformly summable in every closed bounded domain contained in the interior of the star.
(cf. Star of a function element), and it is uniformly summable in every closed bounded domain contained in the interior of the star.
Of the summation methods determined by a transformation of a sequence into a sequence by semi-continuous matrices  of type
of type
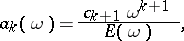 |
where
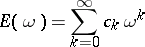 |
is an entire function, Lindelöf considered the case when
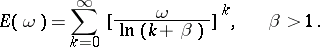 |
A matrix 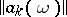 constructed from an entire function of this kind is called a Lindelöf matrix.
constructed from an entire function of this kind is called a Lindelöf matrix.
References
| [1] | E. Lindelöf, J. Math. , 9 (1903) pp. 213–221 |
| [2] | E. Lindelöf, "Le calcul des résidus et ses applications à la théorie des fonctions" , Gauthier-Villars (1905) |
| [3] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [4] | R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950) |
Lindelöf summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lindel%C3%B6f_summation_method&oldid=23394