Difference between revisions of "Lieb-Thirring inequalities"
m (fixing spaces) |
m (fixing > <) |
||
| Line 13: | Line 13: | ||
$$ | $$ | ||
| − | on $L ^ { 2 } ( \mathbf{R} ^ { n } )$, $n \geq 1$. With $e _ { 1 } \leq e _ { 2 } \leq \ | + | on $L ^ { 2 } ( \mathbf{R} ^ { n } )$, $n \geq 1$. With $e _ { 1 } \leq e _ { 2 } \leq \cdots < 0$ denoting the negative eigenvalue(s) of $H$ |
| − | (if any), the Lieb–Thirring inequalities state that for suitable $\gamma \geq 0$ and constants | + | (if any), the Lieb–Thirring inequalities state that for suitable $\gamma \geq 0$ and constants $L_{\gamma,n}$ |
$$ | $$ | ||
| Line 20: | Line 20: | ||
$$ | $$ | ||
| − | with $V _ { - } ( x ) : = \ | + | with $V _ { - } ( x ) : = \max \{ - V ( x ) , 0 \}$. When $\gamma = 0$, the left-hand side is just the number of negative eigenvalues. Such an inequality (a1) can hold if and only if |
$$ | $$ | ||
| Line 26: | Line 26: | ||
$$ | $$ | ||
| − | The cases $\gamma | + | The cases $\gamma > 1 / 2$, $n = 1$, $\gamma > 0$, $n \geq 2$, were established by E.H. Lieb and W.E. Thirring [[#References|[a14]]] in connection with their proof of stability of matter. The case $\gamma = 1 / 2$, $n = 1$, was established by T. Weidl [[#References|[a16]]]. The case $\gamma = 0$, $n \geq 3$, was established independently by M. Cwikel [[#References|[a15]]], Lieb [[#References|[a6]]] and G.V. Rosenbljum [[#References|[a10]]] by different methods and is known as the CLR bound; the smallest known value (as of 1998) for $L _ { 0 , n }$ is in [[#References|[a6]]], [[#References|[a7]]]. Closely associated with the inequality (a1) is the semi-classical approximation for $\sum | e | ^ { \gamma }$, which serves as a heuristic motivation for (a1). It is (cf. [[#References|[a14]]]): |
$$ | $$ | ||
| − | \begin{equation*} \sum _ { j \geq 1 } | | + | \begin{equation*} \sum _ { j \geq 1 } | e_j | ^ { \gamma } &\approx& ( 2 \pi ) ^ { - n } \int _ { {\bf R} ^ { n } \times {\bf R} ^ { n } } [ p ^ { 2 } + V ( x ) ] _ { - } ^ { \gamma } d p d x \\ |
| − | + | &=& L _ { \gamma , n } ^ { c } \int _ { {\bf R} ^ { n } } V _ { - } ( x ) ^ { \gamma + n / 2 } d x, \end{equation*} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
$$ | $$ | ||
| Line 46: | Line 39: | ||
$$ | $$ | ||
| − | Indeed, $L _ { \gamma , n } ^ { c } | + | Indeed, $L _ { \gamma , n } ^ { c } < \infty$ for all $\gamma \geq 0$, whereas (a1) holds only for the range given in (a2). It is easy to prove (by considering $V ( x ) = \lambda W ( x )$ with $W$ smooth and $\lambda \rightarrow \infty$) that |
$$ | $$ | ||
| Line 52: | Line 45: | ||
$$ | $$ | ||
| − | An interesting, and mostly open (1998) problem is to determine the sharp value of the constant | + | An interesting, and mostly open (1998) problem is to determine the sharp value of the constant $L_{\gamma, n}$, especially to find those cases in which $L _ { \gamma , n } = L _ { \gamma , n } ^ { c }$. M. Aizenman and Lieb [[#References|[a3]]] proved that the ratio $R_{\gamma, n}=L_{\gamma,n}/L_{\gamma,n}^c$ is a monotonically non-increasing function of $\gamma$. Thus, if $R _ { \Gamma , n } = 1$ for some $\Gamma$, then $L _ { \gamma , n } = L _ { \gamma , n } ^ { c }$ for all $\gamma \geq \Gamma$. The equality $L _ { \frac { 3 } { 2 } ,\, n } = L _ { \frac { 3 } { 2 } ,\, n } ^ { c }$ was proved for $n = 1$ in [[#References|[a14]]] and for $n > 1$ in [[#References|[a2]]] by A. Laptev and Weidl. (See also [[#References|[a1]]].) |
The following sharp constants are known: | The following sharp constants are known: | ||
| Line 66: | Line 59: | ||
$$ | $$ | ||
| − | for $1 / 2 | + | for $1 / 2 < \gamma < 3 / 2$. Instead of considering all the negative eigenvalues as in (a1), one can consider just $e_1$. Then for $\gamma$ as in (a2), |
$$ | $$ | ||
| Line 72: | Line 65: | ||
$$ | $$ | ||
| − | Clearly, $L _ { \gamma , n } ^ { 1 } \leq L _ { \gamma ,n }$, but equality can hold, as in the cases $\gamma = 1 / 2$ and $3 / 2$ for $n = 1$. Indeed, the conjecture in (a3) amounts to $L _ { \gamma , 1 } ^ { 1 } = L _ { \gamma , 1 }$ for $1 / 2 | + | Clearly, $L _ { \gamma , n } ^ { 1 } \leq L _ { \gamma ,n }$, but equality can hold, as in the cases $\gamma = 1 / 2$ and $3 / 2$ for $n = 1$. Indeed, the conjecture in (a3) amounts to $L _ { \gamma , 1 } ^ { 1 } = L _ { \gamma , 1 }$ for $1 / 2 < \gamma < 3 / 2$. The sharp value (a3) of $L _ { \gamma , n} ^ { 1 }$ is obtained by solving a differential equation [[#References|[a14]]]. |
| − | It has been conjectured that for $n \geq 3$, $L _ { 0 ,\, n } = L _ { 0 ,\, n } ^ { 1 }$. In any case, B. Helffer and D. Robert [[#References|[a12]]] showed that for all $n$ and all $\gamma | + | It has been conjectured that for $n \geq 3$, $L _ { 0 ,\, n } = L _ { 0 ,\, n } ^ { 1 }$. In any case, B. Helffer and D. Robert [[#References|[a12]]] showed that for all $n$ and all $\gamma < 1$, $L _ { \gamma , n } > L _ { \gamma , n } ^ { c }$. |
The sharp constant $L _ { 0 , n } ^ { 1 }$, $n \geq 3$, is related to the sharp constant $S _ { n }$ in the Sobolev inequality | The sharp constant $L _ { 0 , n } ^ { 1 }$, $n \geq 3$, is related to the sharp constant $S _ { n }$ in the Sobolev inequality | ||
| Line 110: | Line 103: | ||
Of course, $\int ( \nabla f ) ^ { 2 } = \int f ( - \Delta f )$. Inequalities of the type (a7) can be found for other powers of $- \Delta$ than the first power. The first example of this kind, due to I. Daubechies [[#References|[a13]]], and one of the most important physically, is to replace $- \Delta$ by $\sqrt { - \Delta }$ in $H$. Then an inequality similar to (a1) holds with $\gamma + n / 2$ replaced by $\gamma + n$ (and with a different $L _ { \gamma , n _ { 1 }}$, of course). Likewise there is an analogue of (a7) with $1 + 2 / n$ replaced by $1 + 1 / n$. | Of course, $\int ( \nabla f ) ^ { 2 } = \int f ( - \Delta f )$. Inequalities of the type (a7) can be found for other powers of $- \Delta$ than the first power. The first example of this kind, due to I. Daubechies [[#References|[a13]]], and one of the most important physically, is to replace $- \Delta$ by $\sqrt { - \Delta }$ in $H$. Then an inequality similar to (a1) holds with $\gamma + n / 2$ replaced by $\gamma + n$ (and with a different $L _ { \gamma , n _ { 1 }}$, of course). Likewise there is an analogue of (a7) with $1 + 2 / n$ replaced by $1 + 1 / n$. | ||
| − | All proofs of (a1) (except [[#References|[a11]]] and [[#References|[a16]]]) actually proceed by finding an upper bound to $N _ { E } ( V )$, the number of eigenvalues of $H = - \Delta + V ( x )$ that are below $- E$. Then, for $\gamma | + | All proofs of (a1) (except [[#References|[a11]]] and [[#References|[a16]]]) actually proceed by finding an upper bound to $N _ { E } ( V )$, the number of eigenvalues of $H = - \Delta + V ( x )$ that are below $- E$. Then, for $\gamma > 0$, |
$$ | $$ | ||
\begin{equation*} \sum | e | ^ { \gamma } = \gamma \int _ { 0 } ^ { \infty } N _ { E } ( V ) E ^ { \gamma - 1 } d E. \end{equation*} | \begin{equation*} \sum | e | ^ { \gamma } = \gamma \int _ { 0 } ^ { \infty } N _ { E } ( V ) E ^ { \gamma - 1 } d E. \end{equation*} | ||
| Line 120: | Line 113: | ||
$$ | $$ | ||
| − | $e | + | $e < 0$ is an eigenvalue of $H$ if and only if $1$ is an eigenvalue of $K _ { |e| } ( V )$. Furthermore, $K _ { E } ( V )$ is operator that is monotone decreasing in $E$, and hence $N _ { E } ( V )$ equals the number of eigenvalues of $K _ { E } ( V )$ that are greater than $1$. |
An important generalization of (a1) is to replace $- \Delta$ in $H$ by $| i \nabla + A ( x ) | ^ { 2 }$, where $A ( x )$ is some arbitrary vector field in ${\bf R} ^ { n }$ (called a magnetic vector potential). Then (a1) still holds, but it is not known if the sharp value of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l120/l120100/l120100119.png"/> changes. What is known is that all presently (1998) known values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l120/l120100/l120100120.png"/> are unchanged. It is also known that $( - \Delta + E ) ^ { - 1 }$, as a kernel in $\mathbf{R} ^ { n } \times \mathbf{R} ^ { n }$, is pointwise greater than the absolute value of the kernel $( | i \nabla + A | ^ { 2 } + E ) ^ { - 1 }$. There is another family of inequalities for orthonormal functions, which is closely related to (a1) and to the CLR bound [[#References|[a9]]]. As before, let $f _ { 1 } , \dots , f _ { N }$ be $N$ orthonormal functions in $L ^ { 2 } ( \mathbf{R} ^ { n } )$ and set | An important generalization of (a1) is to replace $- \Delta$ in $H$ by $| i \nabla + A ( x ) | ^ { 2 }$, where $A ( x )$ is some arbitrary vector field in ${\bf R} ^ { n }$ (called a magnetic vector potential). Then (a1) still holds, but it is not known if the sharp value of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l120/l120100/l120100119.png"/> changes. What is known is that all presently (1998) known values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l120/l120100/l120100120.png"/> are unchanged. It is also known that $( - \Delta + E ) ^ { - 1 }$, as a kernel in $\mathbf{R} ^ { n } \times \mathbf{R} ^ { n }$, is pointwise greater than the absolute value of the kernel $( | i \nabla + A | ^ { 2 } + E ) ^ { - 1 }$. There is another family of inequalities for orthonormal functions, which is closely related to (a1) and to the CLR bound [[#References|[a9]]]. As before, let $f _ { 1 } , \dots , f _ { N }$ be $N$ orthonormal functions in $L ^ { 2 } ( \mathbf{R} ^ { n } )$ and set | ||
| Line 132: | Line 125: | ||
$$ | $$ | ||
| − | $u _ { j }$ is a [[Riesz potential|Riesz potential]] ($m = 0$) or a [[Bessel potential|Bessel potential]] ($m | + | $u _ { j }$ is a [[Riesz potential|Riesz potential]] ($m = 0$) or a [[Bessel potential|Bessel potential]] ($m > 0$) of $f_j$. If $n = 1$ and $m > 0$, then $\rho \in C ^ { 0,1 / 2 } ( \mathbf{R} ^ { n } )$ and $\| \rho \| _ { L^\infty ( {\bf R} )} \leq L / m$. If $n = 2$ and $m > 0$, then for all $1 \leq p < \infty$, $\| \rho \| _ { L ^ { p } ( R ^ { 2 } ) } \leq B _ { p } m ^ { - 2 / p } N ^ { 1 / p }$. If $n \geq 3$, $p = n / ( n - 2 )$ and $m \geq 0$ (including $m = 0$), then $\| \rho \| _ { L ^ { p } ( \mathbf{R} ^ { n } ) } \leq A _ { n } N ^ { 1 / p }$. Here, $L$, $B _ { p }$, $A _ { n }$ are universal constants. Without the orthogonality, $N ^ { 1 / p }$ would have to be replaced by $N$. |
Further generalizations are possible [[#References|[a9]]]. | Further generalizations are possible [[#References|[a9]]]. | ||
Revision as of 04:18, 12 July 2022
Inequalities concerning the negative eigenvalues of the Schrödinger operator (cf. also Schrödinger equation)
$$ \begin{equation*} H = - \Delta + V ( x ) \end{equation*} $$
on $L ^ { 2 } ( \mathbf{R} ^ { n } )$, $n \geq 1$. With $e _ { 1 } \leq e _ { 2 } \leq \cdots < 0$ denoting the negative eigenvalue(s) of $H$ (if any), the Lieb–Thirring inequalities state that for suitable $\gamma \geq 0$ and constants $L_{\gamma,n}$
$$ \begin{equation} \tag{a1} \sum _ { j \geq 1 } | e _ { j } | ^ { \gamma } \leq L _ { \gamma , n } \int _ { \mathbf{R} ^ { n } } V _ { - } ( x ) ^ { \gamma + n / 2 } d x \end{equation} $$
with $V _ { - } ( x ) : = \max \{ - V ( x ) , 0 \}$. When $\gamma = 0$, the left-hand side is just the number of negative eigenvalues. Such an inequality (a1) can hold if and only if
$$ \begin{equation} \tag{a2} \left\{ \begin{array} { l l } { \gamma \geq \frac { 1 } { 2 } } & { \text { for } n= 1, } \\ { \gamma > 0 } & { \text { for }n = 2, } \\ { \gamma \geq 0 } & { \text { for } n\geq 3. } \end{array} \right. \end{equation} $$
The cases $\gamma > 1 / 2$, $n = 1$, $\gamma > 0$, $n \geq 2$, were established by E.H. Lieb and W.E. Thirring [a14] in connection with their proof of stability of matter. The case $\gamma = 1 / 2$, $n = 1$, was established by T. Weidl [a16]. The case $\gamma = 0$, $n \geq 3$, was established independently by M. Cwikel [a15], Lieb [a6] and G.V. Rosenbljum [a10] by different methods and is known as the CLR bound; the smallest known value (as of 1998) for $L _ { 0 , n }$ is in [a6], [a7]. Closely associated with the inequality (a1) is the semi-classical approximation for $\sum | e | ^ { \gamma }$, which serves as a heuristic motivation for (a1). It is (cf. [a14]):
$$ \begin{equation*} \sum _ { j \geq 1 } | e_j | ^ { \gamma } &\approx& ( 2 \pi ) ^ { - n } \int _ { {\bf R} ^ { n } \times {\bf R} ^ { n } } [ p ^ { 2 } + V ( x ) ] _ { - } ^ { \gamma } d p d x \\ &=& L _ { \gamma , n } ^ { c } \int _ { {\bf R} ^ { n } } V _ { - } ( x ) ^ { \gamma + n / 2 } d x, \end{equation*} $$
with
$$ \begin{equation*} L _ { \gamma , n } ^ { c } = 2 ^ { - n } \pi ^ { - n / 2 } \frac { \Gamma ( \gamma + 1 ) } { \Gamma ( \gamma + 1 + n / 2 ) }. \end{equation*} $$
Indeed, $L _ { \gamma , n } ^ { c } < \infty$ for all $\gamma \geq 0$, whereas (a1) holds only for the range given in (a2). It is easy to prove (by considering $V ( x ) = \lambda W ( x )$ with $W$ smooth and $\lambda \rightarrow \infty$) that
$$ \begin{equation*} L _ { \gamma , n } \geq L _ { \gamma , n } ^ { c }. \end{equation*} $$
An interesting, and mostly open (1998) problem is to determine the sharp value of the constant $L_{\gamma, n}$, especially to find those cases in which $L _ { \gamma , n } = L _ { \gamma , n } ^ { c }$. M. Aizenman and Lieb [a3] proved that the ratio $R_{\gamma, n}=L_{\gamma,n}/L_{\gamma,n}^c$ is a monotonically non-increasing function of $\gamma$. Thus, if $R _ { \Gamma , n } = 1$ for some $\Gamma$, then $L _ { \gamma , n } = L _ { \gamma , n } ^ { c }$ for all $\gamma \geq \Gamma$. The equality $L _ { \frac { 3 } { 2 } ,\, n } = L _ { \frac { 3 } { 2 } ,\, n } ^ { c }$ was proved for $n = 1$ in [a14] and for $n > 1$ in [a2] by A. Laptev and Weidl. (See also [a1].)
The following sharp constants are known:
$L _ { \gamma , n } = L _ { \gamma , n } ^ { c }$, all $\gamma \geq 3 / 2$, [a14], [a3], [a2];
$L _ { 1 / 2,1 } = 1 / 2$, [a11].
There is strong support for the conjecture [a14] that
$$ \begin{equation} \tag{a3} L _ { \gamma , 1 } = \frac { 1 } { \sqrt { \pi } ( \gamma - \frac { 1 } { 2 } ) } \frac { \Gamma ( \gamma + 1 ) } { \Gamma ( \gamma + 1 / 2 ) } \left( \frac { \gamma - \frac { 1 } { 2 } } { \gamma + \frac { 1 } { 2 } } \right) ^ { \gamma + 1 / 2 } \end{equation} $$
for $1 / 2 < \gamma < 3 / 2$. Instead of considering all the negative eigenvalues as in (a1), one can consider just $e_1$. Then for $\gamma$ as in (a2),
$$ \begin{equation*} | e _ { 1 } | ^ { \gamma } \leq L _ { \gamma , n } ^ { 1 } \int _ { \mathbf{R} ^ { n } } V _ { - } ( x ) ^ { \gamma + n / 2 } d x. \end{equation*} $$
Clearly, $L _ { \gamma , n } ^ { 1 } \leq L _ { \gamma ,n }$, but equality can hold, as in the cases $\gamma = 1 / 2$ and $3 / 2$ for $n = 1$. Indeed, the conjecture in (a3) amounts to $L _ { \gamma , 1 } ^ { 1 } = L _ { \gamma , 1 }$ for $1 / 2 < \gamma < 3 / 2$. The sharp value (a3) of $L _ { \gamma , n} ^ { 1 }$ is obtained by solving a differential equation [a14].
It has been conjectured that for $n \geq 3$, $L _ { 0 ,\, n } = L _ { 0 ,\, n } ^ { 1 }$. In any case, B. Helffer and D. Robert [a12] showed that for all $n$ and all $\gamma < 1$, $L _ { \gamma , n } > L _ { \gamma , n } ^ { c }$.
The sharp constant $L _ { 0 , n } ^ { 1 }$, $n \geq 3$, is related to the sharp constant $S _ { n }$ in the Sobolev inequality
$$ \begin{equation} \tag{a4} \| \nabla f \| _ {{ L } ^ 2 ( \mathbf{R} ^ { n } ) } \geq S _ { n } \| f \| _ { L ^{ 2 n / ( n - 2 ) } ( \mathbf{R} ^ { n } ) } \end{equation} $$
by $L _ { 0 , n } ^ { 1 } = ( S _ { n } ) ^ { - n }$. By a "duality argument" [a14], the case $\gamma = 1$ in (a1) can be converted into the following bound for the Laplace operator, $\Delta$. This bound is referred to as a Lieb–Thirring kinetic energy inequality and its most important application is to the stability of matter [a8], [a14].
Let $f _ { 1 } , f _ { 2 } , \ldots$ be any orthonormal sequence (finite or infinite, cf. also Orthonormal system) in $L ^ { 2 } ( \mathbf{R} ^ { n } )$ such that $\nabla f _ { j } \in L ^ { 2 } ( \mathbf{R} ^ { n } )$ for all $j \geq 1$. Associated with this sequence is a "density"
$$ \begin{equation} \tag{a5} \rho ( x ) = \sum _ { j \geq 1 } | f _ { j } ( x ) | ^ { 2 }. \end{equation} $$
Then, with $K _ { n } : = n ( 2 / L _ { 1 , n } ) ^ { 2 / n } ( n + 2 ) ^ { - 1 - 2 / n }$,
$$ \begin{equation} \tag{a6} \sum _ { j \geq 1 } \int _ { \mathbf{R} ^ { n } } | \nabla f _ { j } ( x ) | ^ { 2 } d x \geq K _ { n } \int _ { \mathbf{R} ^ { n } } \rho ( x ) ^ { 1 + 2 / n } d x. \end{equation} $$
This can be extended to anti-symmetric functions in $L ^ { 2 } ( \mathbf{R} ^ { n N } )$. If $\Phi = \Phi ( x _ { 1 } , \dots , x _ { N } )$ is such a function, one defines, for $x \in \mathbf{R} ^ { n }$, $$ \begin{equation*} \rho ( x ) = N \int _ { \mathbf{R} ^ { n ( N - 1 ) } } | \Phi ( x , x _ { 2 } , \ldots , x _ { N } ) | ^ { 2 } d x _ { 2 } \ldots d x _ { N }. \end{equation*} $$
Then, if $\int _ { \mathbf{R} ^ { n N } } | \Phi | ^ { 2 } = 1$, $$ \begin{equation} \tag{a7} \int _ { R ^ { n N } } | \nabla \Phi | ^ { 2 } \geq K _ { n } \int _ { {\bf R} ^ { n } } \rho ( x ) ^ { 1 + 2 / n } d x. \end{equation} $$
Note that the choice $\Phi = ( N ! ) ^ { - 1 / 2 } \operatorname { det } f _ { j } ( x _ { k } ) | _ { j , k = 1 } ^ { N }$ with $f_j$ orthonormal reduces the general case (a7) to (a6). If the conjecture $L _ { 1,3 } = L _ { 1,3 } ^ { c }$ is correct, then the bound in (a7) equals the Thomas–Fermi kinetic energy Ansatz (cf. Thomas–Fermi theory), and hence it is a challenge to prove this conjecture. In the meantime, see [a7], [a5] for the best available constants to date (1998).
Of course, $\int ( \nabla f ) ^ { 2 } = \int f ( - \Delta f )$. Inequalities of the type (a7) can be found for other powers of $- \Delta$ than the first power. The first example of this kind, due to I. Daubechies [a13], and one of the most important physically, is to replace $- \Delta$ by $\sqrt { - \Delta }$ in $H$. Then an inequality similar to (a1) holds with $\gamma + n / 2$ replaced by $\gamma + n$ (and with a different $L _ { \gamma , n _ { 1 }}$, of course). Likewise there is an analogue of (a7) with $1 + 2 / n$ replaced by $1 + 1 / n$.
All proofs of (a1) (except [a11] and [a16]) actually proceed by finding an upper bound to $N _ { E } ( V )$, the number of eigenvalues of $H = - \Delta + V ( x )$ that are below $- E$. Then, for $\gamma > 0$, $$ \begin{equation*} \sum | e | ^ { \gamma } = \gamma \int _ { 0 } ^ { \infty } N _ { E } ( V ) E ^ { \gamma - 1 } d E. \end{equation*} $$
Assuming $V = - V _ { - }$ (since $V _ { + }$ only raises the eigenvalues), $N _ { E } ( V )$ is most accessible via the positive semi-definite Birman–Schwinger kernel (cf. [a4]) $$ \begin{equation*} K _ { E } ( V ) = \sqrt { V _ { - } } ( - \Delta + E ) ^ { - 1 } \sqrt { V _ { - } }. \end{equation*} $$
$e < 0$ is an eigenvalue of $H$ if and only if $1$ is an eigenvalue of $K _ { |e| } ( V )$. Furthermore, $K _ { E } ( V )$ is operator that is monotone decreasing in $E$, and hence $N _ { E } ( V )$ equals the number of eigenvalues of $K _ { E } ( V )$ that are greater than $1$.
An important generalization of (a1) is to replace $- \Delta$ in $H$ by $| i \nabla + A ( x ) | ^ { 2 }$, where $A ( x )$ is some arbitrary vector field in ${\bf R} ^ { n }$ (called a magnetic vector potential). Then (a1) still holds, but it is not known if the sharp value of  changes. What is known is that all presently (1998) known values of
changes. What is known is that all presently (1998) known values of 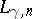 are unchanged. It is also known that $( - \Delta + E ) ^ { - 1 }$, as a kernel in $\mathbf{R} ^ { n } \times \mathbf{R} ^ { n }$, is pointwise greater than the absolute value of the kernel $( | i \nabla + A | ^ { 2 } + E ) ^ { - 1 }$. There is another family of inequalities for orthonormal functions, which is closely related to (a1) and to the CLR bound [a9]. As before, let $f _ { 1 } , \dots , f _ { N }$ be $N$ orthonormal functions in $L ^ { 2 } ( \mathbf{R} ^ { n } )$ and set
are unchanged. It is also known that $( - \Delta + E ) ^ { - 1 }$, as a kernel in $\mathbf{R} ^ { n } \times \mathbf{R} ^ { n }$, is pointwise greater than the absolute value of the kernel $( | i \nabla + A | ^ { 2 } + E ) ^ { - 1 }$. There is another family of inequalities for orthonormal functions, which is closely related to (a1) and to the CLR bound [a9]. As before, let $f _ { 1 } , \dots , f _ { N }$ be $N$ orthonormal functions in $L ^ { 2 } ( \mathbf{R} ^ { n } )$ and set
$$ \begin{equation*} u _ { j } = ( - \Delta + m ^ { 2 } ) ^ { - 1 / 2 } f _ { j }, \end{equation*} $$
$$ \begin{equation*} \rho ( x ) = \sum _ { j = 1 } ^ { N } | u _ { j } ( x ) | ^ { 2 }. \end{equation*} $$
$u _ { j }$ is a Riesz potential ($m = 0$) or a Bessel potential ($m > 0$) of $f_j$. If $n = 1$ and $m > 0$, then $\rho \in C ^ { 0,1 / 2 } ( \mathbf{R} ^ { n } )$ and $\| \rho \| _ { L^\infty ( {\bf R} )} \leq L / m$. If $n = 2$ and $m > 0$, then for all $1 \leq p < \infty$, $\| \rho \| _ { L ^ { p } ( R ^ { 2 } ) } \leq B _ { p } m ^ { - 2 / p } N ^ { 1 / p }$. If $n \geq 3$, $p = n / ( n - 2 )$ and $m \geq 0$ (including $m = 0$), then $\| \rho \| _ { L ^ { p } ( \mathbf{R} ^ { n } ) } \leq A _ { n } N ^ { 1 / p }$. Here, $L$, $B _ { p }$, $A _ { n }$ are universal constants. Without the orthogonality, $N ^ { 1 / p }$ would have to be replaced by $N$.
Further generalizations are possible [a9].
References
| [a1] | R. Benguria, M. Loss, "A simple proof of a theorem of Laptev and Weidl" Preprint (1999) |
| [a2] | A. Laptev, T. Weidl, "Sharp Lieb–Thirring inequalities in high dimensions" Acta Math. (in press 1999) |
| [a3] | M.A. Aizenman, E.H. Lieb, "On semiclassical bounds for eigenvalues of Schrödinger operators" Phys. Lett. , 66A (1978) pp. 427–429 |
| [a4] | B. Simon, "Functional integration and quantum physics" , Pure Appl. Math. , 86 , Acad. Press (1979) |
| [a5] | Ph. Blanchard, J. Stubbe, "Bound states for Schrödinger Hamiltonians: phase space methods and applications" Rev. Math. Phys. , 8 (1996) pp. 503–547 |
| [a6] | E.H. Lieb, "The numbers of bound states of one-body Schrödinger operators and the Weyl problem" , Geometry of the Laplace Operator (Honolulu, 1979) , Proc. Symp. Pure Math. , 36 , Amer. Math. Soc. (1980) pp. 241–251 |
| [a7] | E.H. Lieb, "On characteristic exponents in turbulence" Comm. Math. Phys. , 92 (1984) pp. 473–480 |
| [a8] | E.H. Lieb, "Kinetic energy bounds and their applications to the stability of matter" H. Holden (ed.) A. Jensen (ed.) , Schrödinger Operators (Proc. Nordic Summer School, 1988) , Lecture Notes Physics , 345 , Springer (1989) pp. 371–382 |
| [a9] | E.H. Lieb, "An $L ^ { p }$ bound for the Riesz and Bessel potentials of orthonormal functions" J. Funct. Anal. , 51 (1983) pp. 159–165 |
| [a10] | G.V. Rosenbljum, "Distribution of the discrete spectrum of singular differential operators" Dokl. Akad. Nauk SSSR , 202 (1972) pp. 1012–1015 ((The details are given in: Izv. Vyss. Uchebn. Zaved. Mat. 164 (1976), 75-86 (English transl.: Soviet Math. (Izv. VUZ) 20 (1976), 63-71))) |
| [a11] | D. Hundertmark, E.H. Lieb, L.E. Thomas, "A sharp bound for an eigenvalue moment of the one-dimensional Schrödinger operator" Adv. Theor. Math. Phys. , 2 (1998) pp. 719–731 |
| [a12] | B. Helffer, D. Robert, "Riesz means of bound states and semi-classical limit connected with a Lieb–Thirring conjecture, II" Ann. Inst. H. Poincaré Phys. Th. , 53 (1990) pp. 139–147 |
| [a13] | I. Daubechies, "An uncertainty principle for fermions with generalized kinetic energy" Comm. Math. Phys. , 90 (1983) pp. 511–520 |
| [a14] | E.H. Lieb, W. Thirring, "Inequalities for the moments of the eigenvalues of the Schrödinger Hamiltonian and their relation to Sobolev inequalities" E. Lieb (ed.) B. Simon (ed.) A. Wightman (ed.) , Studies in Mathematical Physics: Essays in Honor of Valentine Bargmann , Princeton Univ. Press (1976) pp. 269–303 ((See also: W. Thirring (ed.), The stability of matter: from the atoms to stars, Selecta of E.H. Lieb, Springer, 1977)) |
| [a15] | M. Cwikel, "Weak type estimates for singular values and the number of bound states of Schrödinger operators" Ann. Math. , 106 (1977) pp. 93–100 |
| [a16] | T. Weidl, "On the Lieb–Thirring constants $L_{ \gamma , 1}$ for $\gamma \geq 1 / 2$" Comm. Math. Phys. , 178 : 1 (1996) pp. 135–146 |
Elliott H. Lieb
Copyright to this article is held by Elliott Lieb.
Lieb-Thirring inequalities. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lieb-Thirring_inequalities&oldid=52486