Liénard-Chipart criterion
From Encyclopedia of Mathematics
A modification of the Routh–Hurwitz criterion, which reduces all calculations in it to the calculation of the principal minors of only even (or only odd) orders of a Hurwitz matrix.
Suppose one is given a polynomial
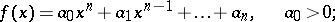 | (*) |
let 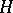 be its Hurwitz matrix (cf. Routh–Hurwitz criterion); let
be its Hurwitz matrix (cf. Routh–Hurwitz criterion); let 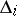 be its principal minor of order
be its principal minor of order 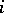 ,
, 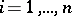 .
.
The Liénard–Chipart criterion: Any of the following four conditions is necessary and sufficient in order that all roots of a polynomial (*) with real coefficients have negative real parts:
1) 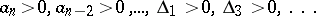 ;
;
2)  ;
;
3) 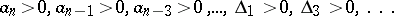 ;
;
4) 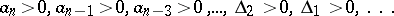 .
.
The criterion was established by A. Liénard and H. Chipart [1].
References
| [1] | A. Liénard, H. Chipart, "Sur la signe de la partie réelle des racines d'une équation algébrique" J. Math. Pures Appl. , 10 (1914) pp. 291–346 |
| [2] | F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1977) (Translated from Russian) |
How to Cite This Entry:
Liénard-Chipart criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Li%C3%A9nard-Chipart_criterion&oldid=15156
Liénard-Chipart criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Li%C3%A9nard-Chipart_criterion&oldid=15156
This article was adapted from an original article by I.V. Proskuryakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article