Lefschetz formula
A formula that expresses the number of fixed points of an endomorphism of a topological space in terms of the traces of the corresponding endomorphisms in the cohomology groups.
This formula was first established by S. Lefschetz for finite-dimensional orientable topological manifolds [1] and for finite cell complexes (see [2], [3]). These papers of Lefschetz were preceded by a paper of L.E.J. Brouwer (1911) on the fixed point of a continuous mapping of an  -dimensional sphere into itself. A new version of the proof of the Lefschetz formula for finite cell complexes was given by H. Hopf (see [9]).
-dimensional sphere into itself. A new version of the proof of the Lefschetz formula for finite cell complexes was given by H. Hopf (see [9]).
Let 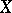 be a connected orientable
be a connected orientable  -dimensional compact topological manifold or an
-dimensional compact topological manifold or an  -dimensional finite cell complex, let
-dimensional finite cell complex, let 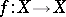 be a continuous mapping and let
be a continuous mapping and let 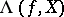 be the Lefschetz number of
be the Lefschetz number of 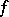 . Assume that all fixed points of the mapping
. Assume that all fixed points of the mapping 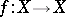 are isolated. For each fixed point
are isolated. For each fixed point 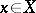 , let
, let 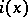 be its Kronecker index (the local degree (cf. Degree of a mapping) of
be its Kronecker index (the local degree (cf. Degree of a mapping) of 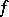 in a neighbourhood of
in a neighbourhood of  ). Then the Lefschetz formula for
). Then the Lefschetz formula for 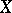 and
and 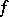 has the form
has the form
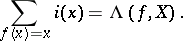 | (1) |
There is, [8], a generalization of the Lefschetz formula to the case of arbitrary continuous mappings of compact Euclidean neighbourhood retracts.
Let 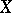 be a differentiable compact orientable manifold and let
be a differentiable compact orientable manifold and let 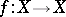 be a differentiable mapping. A fixed point
be a differentiable mapping. A fixed point 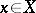 for
for 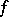 is said to be non-singular if it is isolated and if
is said to be non-singular if it is isolated and if 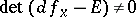 , where
, where 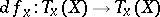 is the differential of
is the differential of 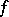 at
at  and
and 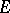 is the identity transformation. For a non-singular point
is the identity transformation. For a non-singular point 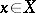 its index
its index 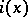 coincides with the number
coincides with the number 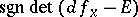 . In this case the Lefschetz formula (1) shows that the Lefschetz number
. In this case the Lefschetz formula (1) shows that the Lefschetz number 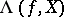 is equal to the difference between the number of fixed points with index
is equal to the difference between the number of fixed points with index 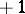 and the number of fixed points with index
and the number of fixed points with index 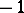 ; in particular, it does not exceed the total number of fixed points. In this case the left-hand side of (1) can be determined in the same way as the intersection index
; in particular, it does not exceed the total number of fixed points. In this case the left-hand side of (1) can be determined in the same way as the intersection index 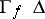 on
on 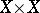 , where
, where 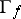 is the graph of
is the graph of 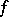 and
and 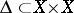 is the diagonal (cf. Intersection index (in algebraic geometry)).
is the diagonal (cf. Intersection index (in algebraic geometry)).
A consequence of the Lefschetz formula is the Hopf formula, which asserts that the Euler characteristic 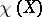 is equal to the sum of the indices of the zeros of a global
is equal to the sum of the indices of the zeros of a global 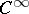 -vector field
-vector field  on
on 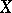 (it is assumed that all zeros of
(it is assumed that all zeros of  are isolated) (see [5]).
are isolated) (see [5]).
There is a version of the Lefschetz formula for compact complex manifolds and the Dolbeault cohomology (see [5]). Let 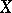 be a compact complex manifold of dimension
be a compact complex manifold of dimension 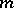 and let
and let 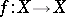 a be holomorphic mapping with non-singular fixed points. Let
a be holomorphic mapping with non-singular fixed points. Let 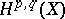 be the Dolbeault cohomology of
be the Dolbeault cohomology of 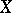 of type
of type 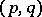 (cf. Differential form) and let
(cf. Differential form) and let 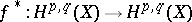 be the endomorphism induced by
be the endomorphism induced by 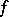 . The number
. The number
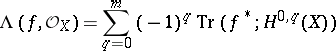 |
is called the holomorphic Lefschetz number. One then has the following holomorphic Lefschetz formula:
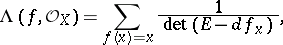 |
where 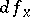 is the holomorphic differential of
is the holomorphic differential of 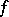 at
at  .
.
In abstract algebraic geometry the Lefschetz formula has served as a starting point in the search for Weil cohomology in connection with Weil's conjectures about zeta-functions of algebraic varieties defined over finite fields (cf. Zeta-function). An analogue of the Lefschetz formula in abstract algebraic geometry has been established for 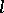 -adic cohomology with compact support and with coefficients in constructible
-adic cohomology with compact support and with coefficients in constructible 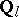 -sheaves, where
-sheaves, where 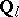 is the field of
is the field of 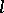 -adic numbers and where
-adic numbers and where 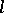 is a prime number distinct from the characteristic of the field
is a prime number distinct from the characteristic of the field 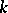 . This formula is often called the trace formula.
. This formula is often called the trace formula.
Let 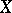 be an algebraic variety (or scheme) over a finite field
be an algebraic variety (or scheme) over a finite field 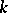 , let
, let 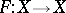 be a Frobenius morphism (cf. e.g. Frobenius automorphism),
be a Frobenius morphism (cf. e.g. Frobenius automorphism), 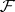 a sheaf on
a sheaf on 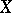 , and let
, and let 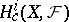 be cohomology with compact support of the variety (scheme)
be cohomology with compact support of the variety (scheme) 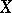 with coefficients in
with coefficients in 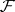 . Then the morphism
. Then the morphism 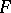 determines a cohomology endomorphism
determines a cohomology endomorphism
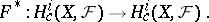 |
If 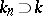 is an extension of
is an extension of 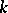 of degree
of degree  and if
and if 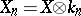 ,
, 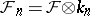 are the variety (scheme) and sheaf obtained from
are the variety (scheme) and sheaf obtained from 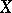 and
and 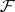 by extending the field of scalars, then the corresponding Frobenius morphism
by extending the field of scalars, then the corresponding Frobenius morphism 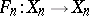 coincides with the
coincides with the  -th power
-th power 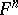 of
of 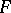 .
.
Now let 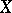 be a separable scheme of finite type over the finite field
be a separable scheme of finite type over the finite field 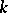 of
of 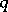 elements, let
elements, let 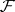 be a constructible
be a constructible 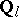 -sheaf on
-sheaf on  ,
, 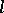 a prime number distinct from the characteristic of
a prime number distinct from the characteristic of 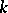 , and
, and 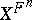 the set of fixed geometric points of the morphism
the set of fixed geometric points of the morphism 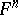 or, equivalently, the set
or, equivalently, the set 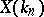 of geometric points of the scheme
of geometric points of the scheme 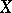 with values in the field
with values in the field 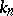 . Then for any integer
. Then for any integer 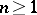 the following Lefschetz formula (or trace formula) holds (see [6], [7]):
the following Lefschetz formula (or trace formula) holds (see [6], [7]):
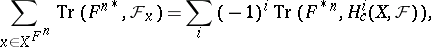 | (2) |
where 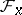 is the stalk of
is the stalk of 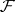 over
over  . In the case of the constant sheaf
. In the case of the constant sheaf 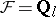 one has
one has 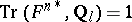 and the left-hand side of (2) is none other than the number of geometric points of
and the left-hand side of (2) is none other than the number of geometric points of 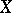 with values in
with values in 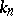 . In particular, for
. In particular, for 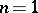 this is simply the number of points of
this is simply the number of points of 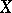 with values in the ground field
with values in the ground field 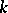 . If
. If 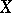 is proper over
is proper over 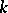 (for example, if
(for example, if 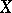 is a complete algebraic variety over
is a complete algebraic variety over 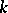 ), then
), then 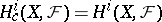 and the right-hand side of (2) is an alternating sum of the traces of the Frobenius endomorphism in the ordinary cohomology of
and the right-hand side of (2) is an alternating sum of the traces of the Frobenius endomorphism in the ordinary cohomology of 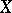 .
.
There are (see [7]) generalizations of formula (2).
References
| [1] | S. Lefschetz, "Intersections and transformations of complexes and manifolds" Trans. Amer. Soc. , 28 (1926) pp. 1–49 |
| [2] | S. Lefschetz, "The residual set of a complex manifold and related questions" Proc. Nat. Acad. Sci. USA , 13 (1927) pp. 614–622 |
| [3] | S. Lefschetz, "On the fixed point formula" Ann. of Math. (2) , 38 (1937) pp. 819–822 |
| [4] | S.L. Kleiman, "Algebraic cycles and the Weil conjectures" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , Dix exposés sur la cohomologie des schémas , North-Holland & Masson (1968) pp. 359–386 |
| [5] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) |
| [6] | P. Deligne, "Cohomologie étale (SGA 4 1/2)" , Lect. notes in math. , 569 , Springer (1977) |
| [7] | A. Grothendieck, I. Bucur, C. Honzel, L. Illusie, J.-P. Jouanolou, J.-P. Serre, "Cohomologie  -adique et fonctions -adique et fonctions  . SGA 5" , Lect. notes in math. , 589 , Springer (1977) . SGA 5" , Lect. notes in math. , 589 , Springer (1977) |
| [8] | A. Dold, "Lectures on algebraic topology" , Springer (1980) |
| [9] | H. Seifert, W. Threlfall, "A textbook of topology" , Acad. Press (1980) (Translated from German) |
Comments
For the Lefschetz formula in abstract algebraic geometry and its generalizations by A. Grothendieck see also [a1].
References
| [a1] | E. Feitag, R. Kiehl, "Etale cohomology and the Weil conjecture" , Springer (1988) |
Lefschetz formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lefschetz_formula&oldid=16459