Difference between revisions of "Lebesgue-Stieltjes integral"
Ulf Rehmann (talk | contribs) m (moved Lebesgue–Stieltjes integral to Lebesgue-Stieltjes integral: ascii title) |
m |
||
| Line 1: | Line 1: | ||
| + | {{TEX|want}} | ||
| + | |||
A generalization of the [[Lebesgue integral|Lebesgue integral]]. For a non-negative measure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057930/l0579301.png" /> the name "Lebesgue–Stieltjes integral" is used in the case when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057930/l0579302.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057930/l0579303.png" /> is not the Lebesgue measure; then the integral <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057930/l0579304.png" /> is defined in the same way as the Lebesgue integral in the general case. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057930/l0579305.png" /> is of variable sign, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057930/l0579306.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057930/l0579307.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057930/l0579308.png" /> are non-negative measures, and the Lebesgue–Stieltjes integral | A generalization of the [[Lebesgue integral|Lebesgue integral]]. For a non-negative measure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057930/l0579301.png" /> the name "Lebesgue–Stieltjes integral" is used in the case when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057930/l0579302.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057930/l0579303.png" /> is not the Lebesgue measure; then the integral <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057930/l0579304.png" /> is defined in the same way as the Lebesgue integral in the general case. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057930/l0579305.png" /> is of variable sign, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057930/l0579306.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057930/l0579307.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057930/l0579308.png" /> are non-negative measures, and the Lebesgue–Stieltjes integral | ||
Revision as of 10:12, 25 February 2013
A generalization of the Lebesgue integral. For a non-negative measure 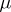 the name "Lebesgue–Stieltjes integral" is used in the case when
the name "Lebesgue–Stieltjes integral" is used in the case when 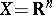 and
and 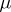 is not the Lebesgue measure; then the integral
is not the Lebesgue measure; then the integral  is defined in the same way as the Lebesgue integral in the general case. If
is defined in the same way as the Lebesgue integral in the general case. If 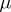 is of variable sign, then
is of variable sign, then 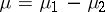 , where
, where  and
and 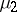 are non-negative measures, and the Lebesgue–Stieltjes integral
are non-negative measures, and the Lebesgue–Stieltjes integral
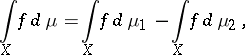 |
under the condition that both integrals on the right-hand side exist. For 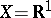 the fact that
the fact that 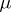 is countably additive and bounded is equivalent to the fact that the measure is generated by some function
is countably additive and bounded is equivalent to the fact that the measure is generated by some function 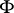 of bounded variation. In this case the Lebesgue–Stieltjes integral is written in the form
of bounded variation. In this case the Lebesgue–Stieltjes integral is written in the form
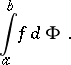 |
For a discrete measure the Lebesgue–Stieltjes integral is a series of numbers.
References
| [1] | E. Kamke, "Das Lebesgue–Stieltjes-Integral" , Teubner (1960) |
Comments
References
| [a1] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) |
Lebesgue-Stieltjes integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lebesgue-Stieltjes_integral&oldid=29489