Lamé curve
From Encyclopedia of Mathematics
A plane algebraic curve whose equation in rectangular Cartesian coordinates has the form
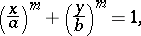 |
where 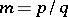 ,
, 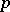 and
and 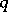 are coprime numbers,
are coprime numbers, 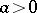 and
and 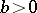 . The order of Lamé's curve is
. The order of Lamé's curve is 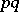 if
if 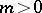 and
and 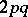 if
if 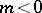 . If
. If 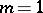 , Lamé's curve is a straight line, if
, Lamé's curve is a straight line, if 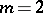 it is an ellipse, and if
it is an ellipse, and if 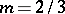 and
and 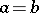 it is an astroid. The Lamé curves are named after G. Lamé, who considered them in 1818.
it is an astroid. The Lamé curves are named after G. Lamé, who considered them in 1818.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
References
| [a1] | K. Fladt, "Analytische Geometrie spezieller ebener Kurven" , Akad. Verlagsgesell. (1962) |
| [a2] | F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971) |
How to Cite This Entry:
Lamé curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lam%C3%A9_curve&oldid=11566
Lamé curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lam%C3%A9_curve&oldid=11566
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article