Lacunary sequence
From Encyclopedia of Mathematics
A sequence of numbers 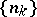 such that
such that 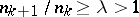 ; this class of sequences is denoted by
; this class of sequences is denoted by  and is used, in particular, in the theory of lacunary series and in the theory of lacunary trigonometric series. There are generalizations of the class
and is used, in particular, in the theory of lacunary series and in the theory of lacunary trigonometric series. There are generalizations of the class 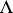 . For example, the class
. For example, the class 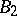 :
: 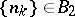 if there is an
if there is an 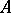 such that the number of solutions of the equations
such that the number of solutions of the equations 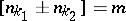 (
(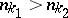 and
and  is the integer part of the number
is the integer part of the number  ) does not exceed
) does not exceed 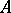 for any integer
for any integer 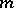 ; the class
; the class 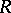 :
: 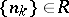 if there is an
if there is an 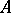 such that the number of solutions of the equations
such that the number of solutions of the equations 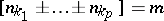 (
(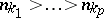 ) does not exceed
) does not exceed 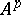 for any
for any 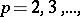 and any integer
and any integer 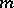 ; and the classes
; and the classes  ,
, 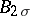 ,
, 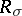 , consisting of sequences that split into finitely-many sequences of the classes
, consisting of sequences that split into finitely-many sequences of the classes 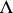 ,
, 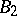 ,
, 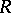 , respectively.
, respectively.
References
| [1] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
How to Cite This Entry:
Lacunary sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lacunary_sequence&oldid=14520
Lacunary sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lacunary_sequence&oldid=14520
This article was adapted from an original article by V.F. Emel'yanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article