L-adic-cohomology
One of the constructions of cohomology of abstract algebraic varieties and schemes. Etale cohomologies (cf. Etale cohomology) of schemes are torsion modules. Cohomology with coefficients in rings of characteristic zero is used for various purposes, mainly in the proof of the Lefschetz formula and its application to zeta-functions. It is obtained from étale cohomology by passing to the projective limit.
Let  be a prime number; an
be a prime number; an  -adic sheaf on a scheme
-adic sheaf on a scheme  is a projective system
is a projective system  of étale Abelian sheaves
of étale Abelian sheaves  such that, for all
such that, for all  , the transfer homomorphisms
, the transfer homomorphisms  are equivalent to the canonical morphism
are equivalent to the canonical morphism 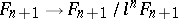 . An
. An 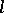 -adic sheaf
-adic sheaf 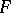 is said to be constructible (respectively, locally constant) if all sheaves
is said to be constructible (respectively, locally constant) if all sheaves 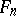 are constructible (locally constant) étale sheaves. There exists a natural equivalence of the category of locally constant constructible sheaves on a connected scheme
are constructible (locally constant) étale sheaves. There exists a natural equivalence of the category of locally constant constructible sheaves on a connected scheme 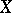 and the category of modules of finite type over the ring
and the category of modules of finite type over the ring 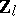 of integral
of integral  -adic numbers which are continuously acted upon from the left by the fundamental group of the scheme
-adic numbers which are continuously acted upon from the left by the fundamental group of the scheme 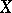 . This proves that locally constant constructible sheaves are abstract analogues of systems of local coefficients in topology. Examples of constructible
. This proves that locally constant constructible sheaves are abstract analogues of systems of local coefficients in topology. Examples of constructible 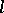 -adic sheaves include the sheaf
-adic sheaves include the sheaf 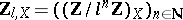 , and the Tate sheaves
, and the Tate sheaves  (where
(where  is the constant sheaf on
is the constant sheaf on 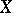 associated with the group
associated with the group 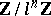 , while
, while 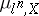 is the sheaf of
is the sheaf of 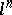 -th power roots of unity on
-th power roots of unity on 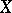 ). If
). If 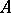 is an Abelian scheme over
is an Abelian scheme over 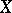 , then
, then 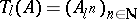 (where
(where  is the kernel of multiplication by
is the kernel of multiplication by 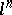 in
in 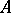 ) forms a locally constant constructible
) forms a locally constant constructible 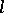 -adic sheaf on
-adic sheaf on 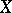 , called the Tate module of
, called the Tate module of 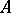 .
.
Let 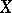 be a scheme over a field
be a scheme over a field 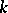 , let
, let 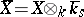 be the scheme obtained from
be the scheme obtained from 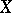 by changing the base from
by changing the base from  to the separable closure
to the separable closure 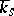 of the field
of the field 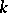 , and let
, and let  be an
be an 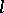 -adic sheaf on
-adic sheaf on 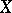 ; the étale cohomology
; the étale cohomology 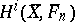 then defines a projective system
then defines a projective system 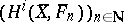 of
of 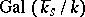 -modules. The projective limit
-modules. The projective limit 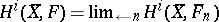 is naturally equipped with the structure of a
is naturally equipped with the structure of a 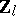 -module on which
-module on which  acts continuously with respect to the
acts continuously with respect to the 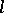 -adic topology. It is called the
-adic topology. It is called the 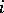 -th
-th 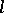 -adic cohomology of the sheaf
-adic cohomology of the sheaf  on
on 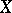 . If
. If  , the usual notation is
, the usual notation is 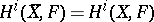 . The fundamental theorems in étale cohomology apply to
. The fundamental theorems in étale cohomology apply to 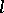 -adic cohomology of constructible
-adic cohomology of constructible 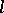 -adic sheaves. If
-adic sheaves. If 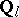 is the field of rational
is the field of rational  -adic numbers, then the
-adic numbers, then the 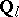 -spaces
-spaces  are called the rational
are called the rational  -adic cohomology of the scheme
-adic cohomology of the scheme 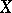 . Their dimensions
. Their dimensions 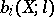 (if defined) are called the
(if defined) are called the  -th Betti numbers of
-th Betti numbers of 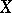 . For complete
. For complete  -schemes the numbers
-schemes the numbers 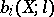 are defined and are independent of
are defined and are independent of 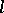 (
( ). If
). If  is an algebraically closed field of characteristic
is an algebraically closed field of characteristic  and if
and if  , then the assignment of the spaces
, then the assignment of the spaces 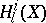 to a smooth complete
to a smooth complete 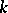 -variety defines a Weil cohomology. If
-variety defines a Weil cohomology. If 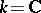 is the field of complex numbers, the comparison theorem
is the field of complex numbers, the comparison theorem 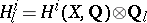 is valid.
is valid.
References
| [1] | A. Grothendieck, "Formule de Lefschetz et rationalité des fonctions  " , Sem. Bourbaki , 17 : 279 (1964–1965) " , Sem. Bourbaki , 17 : 279 (1964–1965) |
Comments
The fact (mentioned above) that for complete  -schemes the Betti numbers are independent of
-schemes the Betti numbers are independent of 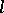 follows from Deligne's proof of the Weil conjectures (cf. also Zeta-function).
follows from Deligne's proof of the Weil conjectures (cf. also Zeta-function).
References
| [a1] | A. Grothendieck, "Cohomologie  -adique et fonctions -adique et fonctions 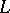 " , SGA 5 , Lect. notes in math. , 589 , Springer (1977) " , SGA 5 , Lect. notes in math. , 589 , Springer (1977) |
| [a2] | J.S. Milne, "Etale cohomology" , Princeton Univ. Press (1980) |
| [a3] | E. Freitag, R. Kiehl, "Etale cohomology and the Weil conjectures" , Springer (1988) |
| [a4] | P. Deligne, "La conjecture de Weil I" Publ. Math. IHES , 43 (1974) pp. 273–307 |
| [a5] | P. Deligne, "La conjecture de Weil II" Publ. Math. IHES , 52 (1980) pp. 137–252 |
L-adic-cohomology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=L-adic-cohomology&oldid=15770