A five-stage Runge–Kutta method with fourth-order accuracy. Applied to the Cauchy problem
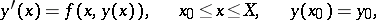 | (1) |
the method is as follows:
 | (2) |
The number 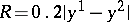 serves as an estimate of the error and is used for automatic selection of the integration step. If
serves as an estimate of the error and is used for automatic selection of the integration step. If  is the prescribed accuracy of the computation, the integration step is selected as follows. First choose some initial step and start the computation by (2) to obtain the number
is the prescribed accuracy of the computation, the integration step is selected as follows. First choose some initial step and start the computation by (2) to obtain the number 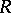 . If
. If 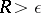 , divide the integration step by 2; if
, divide the integration step by 2; if 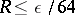 , double it. If
, double it. If  , the selected integration step is satisfactory. Now replace the initial point
, the selected integration step is satisfactory. Now replace the initial point 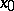 by
by 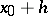 and repeat the entire procedure. This yields an approximate solution
and repeat the entire procedure. This yields an approximate solution 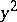 ; the quantity
; the quantity 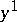 is mainly auxiliary.
is mainly auxiliary.
Since
i.e. the formula for  is as it were "nested" in the formula for
is as it were "nested" in the formula for 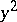 , the method described here for the estimation of the error and the selection of the integration step is known as an imbedded Runge–Kutta method.
, the method described here for the estimation of the error and the selection of the integration step is known as an imbedded Runge–Kutta method.
Standard programs for the Kutta–Merson method are available in Algol [1], [2].
References
| [1] | J. Christiansen, "Numerical solution of ordinary simultaneous differential equations of the 1st order using a method for automatic step change" Numer. Math. , 14 (1970) pp. 317–324 |
| [2] | P.M. Lukehart, "Algorithm 218. Kutta Merson" Comm. Assoc. Comput. Mach. , 6 : 12 (1963) pp. 737–738 |
| [3] | L. Fox, "Numerical solution of ordinary and partial differential equations" , Pergamon (1962) |
| [4] | G.N. Lance, "Numerical methods for high speed computers" , Iliffe (1960) |
Often Runge's name is added: Runge–Kutta–Merson method.
The (Runge–) Kutta–Merson method is due to R.H. Merson [a6]. The order of the numerical approximation defined by 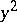 is four and that of the auxiliary (reference) solution
is four and that of the auxiliary (reference) solution 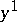 is three. Hence, in general, the difference of these two numerical approximations is only of order three, so that a conservative error estimate results (i.e., it overestimates the local error
is three. Hence, in general, the difference of these two numerical approximations is only of order three, so that a conservative error estimate results (i.e., it overestimates the local error 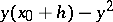 for small
for small 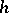 ). However, for linear equations with constant coefficients, a correct estimate of the local error is obtained as
). However, for linear equations with constant coefficients, a correct estimate of the local error is obtained as 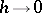 . This can be shown by observing that for linear equations
. This can be shown by observing that for linear equations
Thus,
and
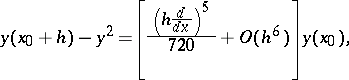 |
so that  equals the local error
equals the local error 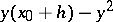 within order
within order 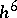 . A further discussion of this method may be found in [a1] and [a5]. A Fortran code of the Kutta–Merson method is available in the NAG library. The Kutta–Merson method is the earliest proposed method belonging to the family of imbedded methods. Higher-order imbedded formulas providing asymptotically-correct approximations to the local error have been derived by E. Fehlberg [a3], [a4]; they have the additional feature that the error constants of the main formula (the formula of highest order) are minimized. However, since the relation between the true (global) error and the local error is generally not known, it is questionable whether one should use the highest-order formula as the main formula, and modern insights advocate to interchange the roles of the main formula and the reference formula (see [a5]). The recently developed imbedded method of J.R. Dormand and P.J. Prince [a2], which combines an eighth-order formula with seventh-order reference formula, is considered as one of the most efficient high-accuracy methods nowadays available [a5].
. A further discussion of this method may be found in [a1] and [a5]. A Fortran code of the Kutta–Merson method is available in the NAG library. The Kutta–Merson method is the earliest proposed method belonging to the family of imbedded methods. Higher-order imbedded formulas providing asymptotically-correct approximations to the local error have been derived by E. Fehlberg [a3], [a4]; they have the additional feature that the error constants of the main formula (the formula of highest order) are minimized. However, since the relation between the true (global) error and the local error is generally not known, it is questionable whether one should use the highest-order formula as the main formula, and modern insights advocate to interchange the roles of the main formula and the reference formula (see [a5]). The recently developed imbedded method of J.R. Dormand and P.J. Prince [a2], which combines an eighth-order formula with seventh-order reference formula, is considered as one of the most efficient high-accuracy methods nowadays available [a5].
References
| [a1] | J.C. Butcher, "The numerical analysis of ordinary differential equations. Runge–Kutta and general linear methods" , Wiley (1987) |
| [a2] | J.R. Dormand, P.J. Prince, "A family of embedded Runge–Kutta formulae" J. Comp. Appl. Math. , 6 (1980) pp. 19–26 |
| [a3] | E. Fehlberg, "Classical fifth-, sixth-, seventh-, and eighth-order Runge–Kutta formulas with stepsize control" NASA Techn. Rep. , 287 (Abstract in: Computing  (1969), 93–106) (1969), 93–106) |
| [a4] | E. Fehlberg, "Low-order classical Runge–Kutta formulas with stepsize control and their application to some heat transfer problems" NASA Techn. Rep. , 315 (Abstract in: Computing  (1969), 61–71) (1969), 61–71) |
| [a5] | E. Hairer, S.P. Nørsett, G. Wanner, "Solving ordinary differential equations" , I. Nonstiff problems , Springer (1987) |
| [a6] | R.H. Merson, "An operational method for the study of integration processes" , Proc. Symp. Data Processing , Weapons Res. Establ. Salisbury , Salisbury (1957) pp. 110–125 |
| [a7] | S.O. Fatunla, "Numerical methods for initial value problems in ordinary differential equations" , Acad. Press (1988) |
How to Cite This Entry:
Kutta-Merson method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kutta-Merson_method&oldid=17685
This article was adapted from an original article by V.V. Pospelov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article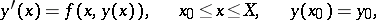

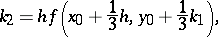
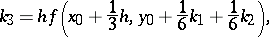
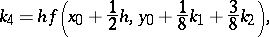
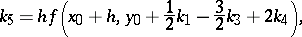
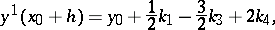
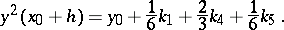
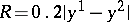 serves as an estimate of the error and is used for automatic selection of the integration step. If
serves as an estimate of the error and is used for automatic selection of the integration step. If  is the prescribed accuracy of the computation, the integration step is selected as follows. First choose some initial step and start the computation by (2) to obtain the number
is the prescribed accuracy of the computation, the integration step is selected as follows. First choose some initial step and start the computation by (2) to obtain the number 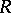 . If
. If 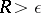 , divide the integration step by 2; if
, divide the integration step by 2; if 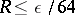 , double it. If
, double it. If  , the selected integration step is satisfactory. Now replace the initial point
, the selected integration step is satisfactory. Now replace the initial point 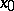 by
by 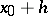 and repeat the entire procedure. This yields an approximate solution
and repeat the entire procedure. This yields an approximate solution 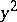 ; the quantity
; the quantity 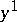 is mainly auxiliary.
is mainly auxiliary.

 is as it were "nested" in the formula for
is as it were "nested" in the formula for 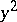 , the method described here for the estimation of the error and the selection of the integration step is known as an imbedded Runge–Kutta method.
, the method described here for the estimation of the error and the selection of the integration step is known as an imbedded Runge–Kutta method.
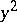 is four and that of the auxiliary (reference) solution
is four and that of the auxiliary (reference) solution 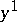 is three. Hence, in general, the difference of these two numerical approximations is only of order three, so that a conservative error estimate results (i.e., it overestimates the local error
is three. Hence, in general, the difference of these two numerical approximations is only of order three, so that a conservative error estimate results (i.e., it overestimates the local error 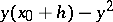 for small
for small 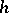 ). However, for linear equations with constant coefficients, a correct estimate of the local error is obtained as
). However, for linear equations with constant coefficients, a correct estimate of the local error is obtained as 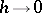 . This can be shown by observing that for linear equations
. This can be shown by observing that for linear equations
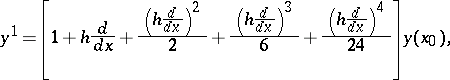



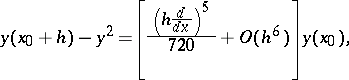
 equals the local error
equals the local error 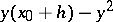 within order
within order 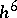 . A further discussion of this method may be found in [a1] and [a5]. A Fortran code of the Kutta–Merson method is available in the NAG library. The Kutta–Merson method is the earliest proposed method belonging to the family of imbedded methods. Higher-order imbedded formulas providing asymptotically-correct approximations to the local error have been derived by E. Fehlberg [a3], [a4]; they have the additional feature that the error constants of the main formula (the formula of highest order) are minimized. However, since the relation between the true (global) error and the local error is generally not known, it is questionable whether one should use the highest-order formula as the main formula, and modern insights advocate to interchange the roles of the main formula and the reference formula (see [a5]). The recently developed imbedded method of J.R. Dormand and P.J. Prince [a2], which combines an eighth-order formula with seventh-order reference formula, is considered as one of the most efficient high-accuracy methods nowadays available [a5].
. A further discussion of this method may be found in [a1] and [a5]. A Fortran code of the Kutta–Merson method is available in the NAG library. The Kutta–Merson method is the earliest proposed method belonging to the family of imbedded methods. Higher-order imbedded formulas providing asymptotically-correct approximations to the local error have been derived by E. Fehlberg [a3], [a4]; they have the additional feature that the error constants of the main formula (the formula of highest order) are minimized. However, since the relation between the true (global) error and the local error is generally not known, it is questionable whether one should use the highest-order formula as the main formula, and modern insights advocate to interchange the roles of the main formula and the reference formula (see [a5]). The recently developed imbedded method of J.R. Dormand and P.J. Prince [a2], which combines an eighth-order formula with seventh-order reference formula, is considered as one of the most efficient high-accuracy methods nowadays available [a5].
 (1969), 93–106)
(1969), 93–106) (1969), 61–71)
(1969), 61–71)