Kullback-Leibler information
Kullback–Leibler quantity of information, Kullback–Leibler information quantity, directed divergence
For discrete distributions (cf. Discrete distribution) given by probability vectors  ,
,  , the Kullback–Leibler (quantity of) information of
, the Kullback–Leibler (quantity of) information of  with respect to
with respect to  is:
is:
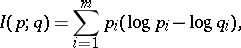 |
where  is the natural logarithm (cf. also Logarithm of a number).
is the natural logarithm (cf. also Logarithm of a number).
More generally, one has:
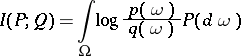 |
for probability distributions  and
and  with densities
with densities 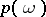 and
and 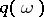 (cf. Density of a probability distribution).
(cf. Density of a probability distribution).
The negative of 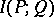 is the conditional entropy (or relative entropy) of
is the conditional entropy (or relative entropy) of  with respect to
with respect to 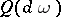 ; see Entropy.
; see Entropy.
Various notions of (asymmetric and symmetric) information distances are based on the Kullback–Leibler information.
The quantity 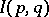 is also called the informational divergence (see Huffman code).
is also called the informational divergence (see Huffman code).
See also Information distance; Kullback–Leibler-type distance measures.
References
| [a1] | S. Kullback, "Information theory and statistics" , Wiley (1959) |
| [a2] | S. Kullback, R.A. Leibler, "On information and sufficiency" Ann. Math. Stat. , 22 (1951) pp. 79–86 |
| [a3] | J. Sakamoto, M. Ishiguro, G. Kitagawa, "Akaike information criterion statistics" , Reidel (1986) |
Kullback-Leibler information. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kullback-Leibler_information&oldid=22681