Korn inequality
From Encyclopedia of Mathematics
An inequality for vector functions 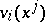 ,
, 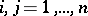 , and their derivatives, defined in some bounded domain
, and their derivatives, defined in some bounded domain 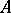 of
of 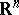 :
:
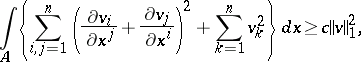 | (1) |
where
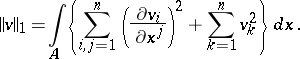 | (2) |
The Korn inequality is also valid for vector functions in the space 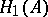 obtained by completing the space
obtained by completing the space 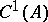 with respect to the norm (2). The inequality (1) is sometimes called the second Korn inequality; the first Korn inequality being inequality (1) without the second term on the left.
with respect to the norm (2). The inequality (1) is sometimes called the second Korn inequality; the first Korn inequality being inequality (1) without the second term on the left.
The inequality was proposed by A. Korn (1908) in order to obtain an a priori estimate for the solution of non-homogeneous equations of elasticity theory.
References
| [1] | G. Fichera, "Existence theorems in elasticity theory" , Handbuch der Physik , VIa/2 , Springer (1972) pp. 347–389 |
How to Cite This Entry:
Korn inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Korn_inequality&oldid=17384
Korn inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Korn_inequality&oldid=17384
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article