Kontorovich-Lebedev transform
Lebedev–Kontorovich transform
 |
where 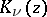 is the Macdonald function.
is the Macdonald function.
This transform was introduced in [a1] and later investigated in [a2]. If 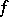 is an integrable function with the weight
is an integrable function with the weight 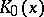 , i.e.
, i.e. 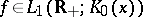 , then
, then 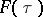 is a bounded continuous function, which tends to zero at infinity (an analogue of the Riemann–Lebesgue lemma, cf. Fourier series, for the Fourier integral). If
is a bounded continuous function, which tends to zero at infinity (an analogue of the Riemann–Lebesgue lemma, cf. Fourier series, for the Fourier integral). If 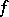 is a function of bounded variation in a neighbourhood of a point
is a function of bounded variation in a neighbourhood of a point 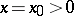 and if
and if
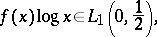 |
 |
then the following inversion formula holds:
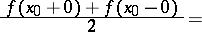 |
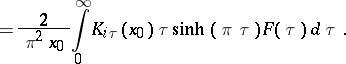 |
If the Mellin transform of 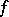 , denoted by
, denoted by 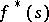 , belongs to the space
, belongs to the space 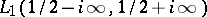 , then
, then 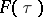 can be represented by an integral (see [a6]):
can be represented by an integral (see [a6]):
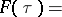 |
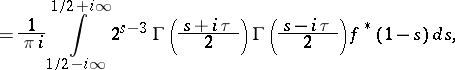 |
where 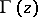 is the Euler gamma-function.
is the Euler gamma-function.
Let 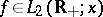 . Then the integral
. Then the integral 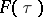 converges in mean square and isomorphically maps the space
converges in mean square and isomorphically maps the space 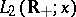 onto the space
onto the space 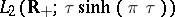 . The inverse operator has the form [a10]
. The inverse operator has the form [a10]
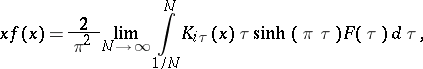 |
and the Parseval equality holds (see also [a3], [a5]):
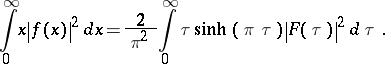 |
The Kontorovich–Lebedev transform of distributions was considered in [a7], [a8]. A transform table for the Kontorovich–Lebedev transform can be found in [a4]. Special properties in 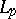 -spaces are given in [a10].
-spaces are given in [a10].
For two functions 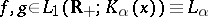 ,
, 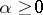 , define the operator of convolution for the Kontorovich–Lebedev transform as ([a9], [a10])
, define the operator of convolution for the Kontorovich–Lebedev transform as ([a9], [a10])
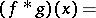 |
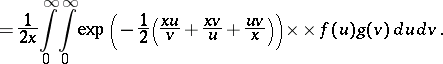 |
The following norm estimate is true:
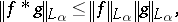 |
and the space 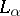 forms a normed ring with the convolution
forms a normed ring with the convolution 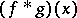 as operation of multiplication.
as operation of multiplication.
If 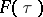 ,
, 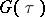 are the Kontorovich–Lebedev transforms of two functions
are the Kontorovich–Lebedev transforms of two functions 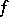 ,
, 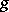 , then the factorization property is true:
, then the factorization property is true:
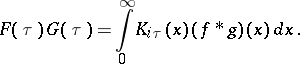 |
If 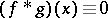 in the ring
in the ring 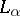 , then at least one of the functions
, then at least one of the functions 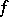 ,
, 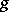 is equal to zero almost-everywhere on
is equal to zero almost-everywhere on 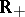 (an analogue of the Titchmarsh theorem).
(an analogue of the Titchmarsh theorem).
The Kontorovich–Lebedev transform is the simplest and most basic in the class of integral transforms of non-convolution type, which forms a special class of so-called index transforms (cf. also Index transform), depending upon parameters, subscripts (indices) of the hypergeometric functions (cf. Hypergeometric function) as kernels.
References
| [a1] | M.I. Kontorovich, N.N. Lebedev, "A method for the solution of problems in diffraction theory and related topics" Zh. Eksper. Teor. Fiz. , 8 : 10–11 (1938) pp. 1192–1206 (In Russian) |
| [a2] | N.N. Lebedev, "Sur une formule d'inversion" Dokl. Akad. Sci. USSR , 52 (1946) pp. 655–658 |
| [a3] | N.N. Lebedev, "Analog of the Parseval theorem for the one integral transform" Dokl. Akad. Nauk SSSR , 68 : 4 (1949) pp. 653–656 (In Russian) |
| [a4] | A. Erdélyi, W. Magnus, F. Oberhettinger, "Tables of integral transforms 1-2" , McGraw-Hill (1954) pp. Chap. XII |
| [a5] | I.N. Sneddon, "The use of integral transforms" , McGraw-Hill (1972) pp. Chap. 6 |
| [a6] | Vu Kim Tuan, S.B. Yakubovich, "The Kontorovich–Lebedev transform in a new class of functions" Amer. Math. Soc. Transl. , 137 (1987) pp. 61–65 |
| [a7] | S.B. Yakubovich, B. Fisher, "On the Kontorovich–Lebedev transformation on distributions" Proc. Amer. Math. Soc. , 122 : 3 (1994) pp. 773–777 |
| [a8] | A.H. Zemanian, "The Kontorovich–Lebedev transformation on distributions of compact support and its inversion" Math. Proc. Cambridge Philos. Soc. , 77 (1975) pp. 139–143 |
| [a9] | S.B. Yakubovich, Yu.F. Luchko, "The hypergeometric approach to integral transforms and convolutions" , Kluwer Acad. Publ. (1994) pp. Chap. 6 |
| [a10] | S.B. Yakubovich, "Index transforms" , World Sci. (1996) pp. Chaps. 2;4 |
Kontorovich-Lebedev transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kontorovich-Lebedev_transform&oldid=14806