Koebe theorem
Koebe's covering theorem: There exist an absolute constant  (the Koebe constant) such that if
(the Koebe constant) such that if  (where
(where 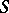 is the class of functions
is the class of functions 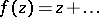 that are regular and univalent in
that are regular and univalent in 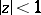 ), then the set of values of the function
), then the set of values of the function 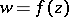 for
for 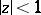 fills out the disc
fills out the disc 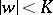 , where
, where 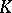 is the largest number for which this holds. L. Bieberbach (1916) proved that
is the largest number for which this holds. L. Bieberbach (1916) proved that 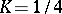 and that on the circle
and that on the circle 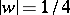 there exists points not belonging to the image of the disc
there exists points not belonging to the image of the disc 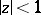 under
under 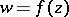 only when
only when
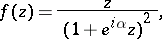 |
where  is a real number. Koebe's covering theorem is sometimes stated as follows: If a function
is a real number. Koebe's covering theorem is sometimes stated as follows: If a function 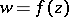 ,
,  , is regular and univalent in
, is regular and univalent in 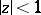 and maps the disc
and maps the disc 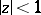 onto a domain not containing the point
onto a domain not containing the point  , then
, then  .
.
Koebe's distortion theorems.
a) There exist positive numbers 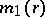 ,
, 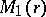 , depending only on
, depending only on  , such that for any
, such that for any  ,
,  ,
,
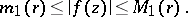 |
b) There exists a number  , depending only on
, depending only on  , such that for
, such that for  ,
, 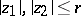 ,
,
 |
This theorem can also be stated as follows: There exist positive numbers 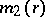 ,
,  , depending only on
, depending only on  , such that for any
, such that for any  ,
,  ,
,
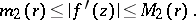 |
Bieberbach proved that the best possible bounds in Koebe's distortion theorems are:
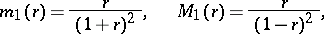 |
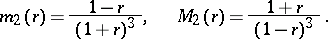 |
Koebe's theorems on mapping finitely-connected domains onto canonical domains.
a) Every  -connected domain
-connected domain 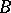 of the
of the  -plane can be univalently mapped onto a circular domain (that is, onto a domain bounded by a finite number of complete non-intersecting circles; here some of the circles may degenerate to a point) of the
-plane can be univalently mapped onto a circular domain (that is, onto a domain bounded by a finite number of complete non-intersecting circles; here some of the circles may degenerate to a point) of the 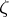 -plane. There exists just one normalized mapping among these mappings taking a given point
-plane. There exists just one normalized mapping among these mappings taking a given point 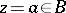 to
to  and such that the expansion of the mapping function in a neighbourhood of
and such that the expansion of the mapping function in a neighbourhood of  has the form
has the form
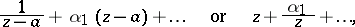 |
according as  is finite or not.
is finite or not.
b) Every  -connected domain
-connected domain  of the
of the  -plane with boundary continua
-plane with boundary continua 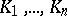 can be univalently mapped onto the
can be univalently mapped onto the 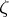 -plane with
-plane with  slits along arcs of logarithmic spirals with respective inclinations
slits along arcs of logarithmic spirals with respective inclinations 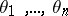 ,
, 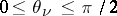 ,
,  , to the radial directions, and, moreover, such that the continuum
, to the radial directions, and, moreover, such that the continuum 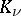 ,
,  , is taken to the arc with inclination
, is taken to the arc with inclination 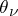 , the given points
, the given points  are taken to
are taken to  and
and 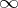 , and the expansion of the mapping function in a neighbourhood of
, and the expansion of the mapping function in a neighbourhood of  has the form
has the form
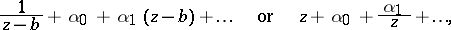 |
according as 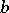 is finite or not. The mapping is unique.
is finite or not. The mapping is unique.
Theorems 1)–3) were established by P. Koebe (see –[4]).
References
| [1a] | P. Koebe, "Ueber die Uniformisierung beliebiger analytischer Kurven" Nachr. K. Ges. Wissenschaft. Göttingen Math. Phys. Kl. , 2 (1907) pp. 191–210 |
| [1b] | P. Koebe, "Ueber die Uniformisierung der algebraischen Kurven durch automorphe Funktionen mit imaginären Substitutionsgruppe" Nachr. K. Ges. Wissenschaft. Göttingen Math. Phys. Kl. , 4 (1908) pp. 68–76 |
| [2] | P. Koebe, "Ueber die Uniformisierung der algebraischen Kurven II" Math. Ann. , 69 (1910) pp. 1–81 |
| [3] | P. Koebe, "Abhandlung zur Theorie der konformen Abbildung IV" Acta Math. , 41 (1918) pp. 305–344 |
| [4] | P. Koebe, "Abhandlung zur Theorie der konformen Abbildung V" Math. Z , 2 (1918) pp. 198–236 |
| [5] | G.M. Goluzin, "Intrinsic problems in the theory of univalent functions" Uspekhi Mat. Nauk , 6 (1939) pp. 26–89 (In Russian) |
| [6] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [7] | J.A. Jenkins, "Univalent functions and conformal mapping" , Springer (1958) |
Comments
Koebe's covering theorem is related to Bloch's theorem: There exists an absolute constant 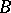 such that if
such that if 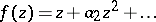 is analytic in
is analytic in  , then
, then  contains a disc of radius
contains a disc of radius  which is the one-to-one image of a subdomain of
which is the one-to-one image of a subdomain of 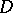 . The best (largest) value of
. The best (largest) value of  is called Bloch's constant. It is known that
is called Bloch's constant. It is known that
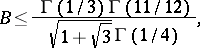 |
and equality has been conjectured. For an up-to-date discussion of these matters, see [a1].
See also Landau theorems.
References
| [a1] | C.D. Minda, "Bloch constants" J. d'Anal. Math. , 41 (1982) pp. 54–84 |
| [a2] | J.B. Conway, "Functions of a complex variable" , Springer (1978) |
Koebe theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Koebe_theorem&oldid=47511