Kobayashi hyperbolicity
domain without large complex discs
Kobayashi hyperbolicity describes in a precise sense whether a complex manifold contains arbitrarily large copies of a one-dimensional complex disc. Extreme examples are the complex disc and the whole complex plane. The former is an example of a Kobayashi-hyperbolic manifold while the latter has arbitrarily large discs in it and is not Kobayashi hyperbolic.
Denote by  the unit disc in the complex plane
the unit disc in the complex plane  .
.
Let  be a complex manifold,
be a complex manifold,  a point in
a point in  and
and 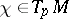 a tangent vector. Consider any holomorphic mapping
a tangent vector. Consider any holomorphic mapping  with
with  ,
,  . The infinitesimal Kobayashi pseudo-metric is defined by
. The infinitesimal Kobayashi pseudo-metric is defined by
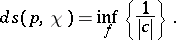 |
The complex manifold 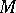 is said to be Kobayashi hyperbolic if
is said to be Kobayashi hyperbolic if  is locally bounded below by a strictly positive constant as
is locally bounded below by a strictly positive constant as 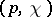 varies over the tangent bundle,
varies over the tangent bundle, 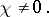
General references for this area are: [a1], [a2] and [a3].
Examples.
1) The unit disc 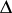 . In this case the Kobayashi pseudo-metric coincides with the Poincaré metric (cf. also Poincaré model).
. In this case the Kobayashi pseudo-metric coincides with the Poincaré metric (cf. also Poincaré model).
2) More generally than Example 1), any bounded domain in 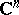 is Kobayashi hyperbolic.
is Kobayashi hyperbolic.
3) At the opposite end, the Kobayashi pseudo-metric of the complex plane 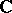 as well as
as well as 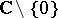 vanishes identically.
vanishes identically.
4) On the other hand, 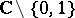 is again Kobayashi hyperbolic. The reason for this is that there is a covering of
is again Kobayashi hyperbolic. The reason for this is that there is a covering of 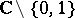 by the unit disc, and coverings are isometries.
by the unit disc, and coverings are isometries.
5) The remarkable Brody theorem states that a compact complex manifold 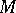 of any dimension is Kobayashi hyperbolic if and only if there is no non-constant holomorphic mapping of
of any dimension is Kobayashi hyperbolic if and only if there is no non-constant holomorphic mapping of 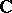 to
to  .
.
The proof of this theorem starts, assuming non-hyperbolicity, with a sequence of holomorphic mappings of the unit disc to 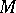 with derivatives at
with derivatives at  converging to infinity. Next one does a suitable scaling to normalize to a sequence which has derivative of length one at
converging to infinity. Next one does a suitable scaling to normalize to a sequence which has derivative of length one at  and which converges to a mapping on the whole plane.
and which converges to a mapping on the whole plane.
6) Generalizations of 4) and 5) have been obtained by M. Green, see [a2], who gave some criteria ensuring that the complement of a finite family of complex hypersurfaces in complex projective space is Kobayashi hyperbolic.
7) The hyperbolicity of 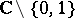 has traditionally been a useful tool in complex dynamics in one dimension. Recently, Kobayashi hyperbolicity has been used in complex dynamics in higher dimensions. For example, T. Ueda, see [a3], showed that all Fatou components, i.e. sets of normality of iterates, of a holomorphic mapping on
has traditionally been a useful tool in complex dynamics in one dimension. Recently, Kobayashi hyperbolicity has been used in complex dynamics in higher dimensions. For example, T. Ueda, see [a3], showed that all Fatou components, i.e. sets of normality of iterates, of a holomorphic mapping on 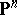 are Kobayashi hyperbolic.
are Kobayashi hyperbolic.
References
| [a1] | S. Kobayashi, "Hyperbolic manifolds and holomorphic mappings" , M. Dekker (1970) |
| [a2] | S. Lang, "Introduction to complex hyperbolic spaces" , Springer (1987) |
| [a3] | J.E. Fornæss, "Dynamics in several complex variables" , CMBS , 87 , Amer. Math. Soc. (1996) |
Kobayashi hyperbolicity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kobayashi_hyperbolicity&oldid=16571