Kneser-Tits hypothesis
Kneser–Tits conjecture
A conjecture on the structure of the 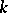 -simple simply-connected algebraic groups that are isotropic over a field
-simple simply-connected algebraic groups that are isotropic over a field 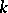 . Namely, the Kneser–Tits conjecture states that the group
. Namely, the Kneser–Tits conjecture states that the group 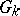 of
of 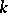 -rational points of a
-rational points of a 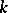 -simple simply-connected isotropic algebraic group
-simple simply-connected isotropic algebraic group 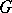 over a field
over a field 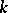 is generated by its unipotent elements. This conjecture was stated in a somewhat less general form by M. Kneser; the general statement is due to J. Tits [1]. For a group of type
is generated by its unipotent elements. This conjecture was stated in a somewhat less general form by M. Kneser; the general statement is due to J. Tits [1]. For a group of type 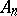 (see Semi-simple algebraic group) the Kneser–Tits conjecture is equivalent to the Tannaka–Artin problem: Does the group
(see Semi-simple algebraic group) the Kneser–Tits conjecture is equivalent to the Tannaka–Artin problem: Does the group 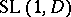 of elements of reduced norm one of a finite-dimensional skew-field
of elements of reduced norm one of a finite-dimensional skew-field 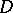 coincide with the commutator subgroup
coincide with the commutator subgroup 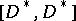 of its multiplicative group
of its multiplicative group 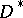 ? The Kneser–Tits conjecture has a close connection with questions of approximation in algebraic groups, rationality of group varieties and algebraic
? The Kneser–Tits conjecture has a close connection with questions of approximation in algebraic groups, rationality of group varieties and algebraic 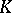 -theory.
-theory.
The Kneser–Tits conjecture has been proved for the case of locally compact fields [2] and also for global function fields [3]. Moreover, for global fields of characteristic zero the method of descent in [2] led to a proof of the Kneser–Tits conjecture for all algebraic groups except for those of types 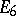 and
and 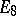 . However, the Kneser–Tits conjecture is not true in general, as follows from the negative solution to the Tannaka–Artin problem [4]. As a result of this, progress has been made on the problem of the investigation of the measure of deviation of
. However, the Kneser–Tits conjecture is not true in general, as follows from the negative solution to the Tannaka–Artin problem [4]. As a result of this, progress has been made on the problem of the investigation of the measure of deviation of  from
from 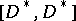 , which is expressible by the reduced Whitehead group (cf. also Linear group). The results obtained along these lines ([5]–[6]) form the basis of reduced
, which is expressible by the reduced Whitehead group (cf. also Linear group). The results obtained along these lines ([5]–[6]) form the basis of reduced  -theory. It has been proved in [7] that the Kneser–Tits conjecture is also false for unitary groups, which in turn opens up a path for the development of reduced unitary
-theory. It has been proved in [7] that the Kneser–Tits conjecture is also false for unitary groups, which in turn opens up a path for the development of reduced unitary 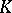 -theory.
-theory.
References
| [1] | J. Tits, "Algebraic and abstract simple groups" Ann. of Math. , 80 : 2 (1964) pp. 313–329 |
| [2] | V.P. Platonov, "The problem of strong approximation and the Kneser–Tits conjecture for algebraic groups" Math. USSR Izv. , 3 : 6 (1969) pp. 1135–1148 Izv. Akad. Nauk SSSR. Ser. Mat. , 33 : 6 (1969) pp. 1121–1220 |
| [3] | V.P. Platonov, "Arithmetic and structural problems in linear algebraic groups" Transl. Amer. Math. Soc. (2) , 109 (1977) pp. 21–26 Proc. Internat. Congr. Mathematicians Vancouver (1974) pp. 471–476 |
| [4] | V.P. Platonov, "On the Tannaka–Artin problem" Soviet Math. Dokl. , 16 (1975) pp. 468–473 Dokl. Akad. Nauk SSSR , 221 : 5 (1975) pp. 1038–1041 |
| [5] | V.P. Platonov, "The Tannaka–Artin problem and reduced 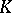 -theory" Math. USSR Izv. , 40 : 2 (1976) pp. 211–244 Izv. Akad, Nauk SSSR. Ser. Mat. , 40 : 2 (1976) pp. 227–261 -theory" Math. USSR Izv. , 40 : 2 (1976) pp. 211–244 Izv. Akad, Nauk SSSR. Ser. Mat. , 40 : 2 (1976) pp. 227–261 |
| [6] | V.P. Platonov, "The infinitude of the reduced Whitehead group in the Tannaka–Artin problem" Math. USSR Sb. , 29 (1976) pp. 167–176 Mat. Sb. , 100 : 2 (1976) pp. 191–200 |
| [7] | V.P. Platonov, V.I. Yanchevskii, "On the Kneser–Tits conjecture for unitary groups" Soviet Math. Dokl. , 16 (1975) pp. 1456–1460 Dokl. Akad. Nauk SSSR , 225 : 1 (1975) pp. 48–51 |
Comments
References
| [a1] | G. Prasad, M.S. Raghunathan, "On the Kneser–Tits problem" Math. Helv. , 60 (1985) pp. 107–121 |
| [a2] | J. Tits, "Groupes de Whitehead de groupes algébriques simples sur un corps (d'après V.P. Platonov et al.)" , Sem. Bourbaki Exp. 505 (1976/77) , Lect. notes in math. , 677 , Springer (1978) pp. 218–236 |
Kneser-Tits hypothesis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kneser-Tits_hypothesis&oldid=13473