Kawamata-Viehweg vanishing theorem
Let  be a connected complex projective manifold (cf. Projective scheme). Let
be a connected complex projective manifold (cf. Projective scheme). Let  denote the canonical bundle of
denote the canonical bundle of  , i.e., the determinant bundle of the cotangent bundle (cf. Tangent bundle) of
, i.e., the determinant bundle of the cotangent bundle (cf. Tangent bundle) of  . A line bundle
. A line bundle  on
on  (cf. also Vector bundle) is said to be nef if the degree of the restriction of
(cf. also Vector bundle) is said to be nef if the degree of the restriction of  to any effective curve on
to any effective curve on  is non-negative. A line bundle is said to be big if the sections of some positive power of
is non-negative. A line bundle is said to be big if the sections of some positive power of  give a birational mapping of
give a birational mapping of 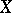 into projective space. For a nef line bundle
into projective space. For a nef line bundle  on
on 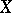 , bigness is equivalent to
, bigness is equivalent to 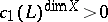 , where
, where 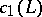 denotes the first Chern class of
denotes the first Chern class of  . Let
. Let 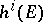 be the dimension of the
be the dimension of the 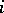 th cohomology group of the sheaf of germs of algebraic or analytic sections of an algebraic line bundle
th cohomology group of the sheaf of germs of algebraic or analytic sections of an algebraic line bundle  on a projective variety. The Kawamata–Viehweg vanishing theorem states that for a nef and big line bundle on a complex projective manifold
on a projective variety. The Kawamata–Viehweg vanishing theorem states that for a nef and big line bundle on a complex projective manifold 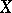 ,
,
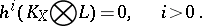 |
When  is a complex compact curve of genus
is a complex compact curve of genus  , the bigness of a line bundle
, the bigness of a line bundle 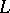 is equivalent to the line bundle being ample (cf. also Ample vector bundle), and since
is equivalent to the line bundle being ample (cf. also Ample vector bundle), and since 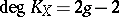 , the Kawamata–Viehweg vanishing theorem takes the form
, the Kawamata–Viehweg vanishing theorem takes the form  if
if 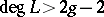 ; or, equivalently,
; or, equivalently, 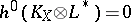 if
if  . For
. For 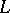 with at least one not-identically-zero section, this vanishing theorem is equivalent to the Roch identification [a15], of the number now (1998) denoted by
with at least one not-identically-zero section, this vanishing theorem is equivalent to the Roch identification [a15], of the number now (1998) denoted by 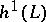 with
with 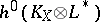 , i.e., the one-dimensional Serre duality theorem. In the late 19th century, the numbers
, i.e., the one-dimensional Serre duality theorem. In the late 19th century, the numbers  intervened in geometric arguments in much the same way as they intervene today, e.g., [a3]. For a very ample line bundle
intervened in geometric arguments in much the same way as they intervene today, e.g., [a3]. For a very ample line bundle  on a two-dimensional complex projective manifold, the Kawamata–Viehweg vanishing theorem was well known as the Picard theorem on the regularity of the adjoint, [a13], Vol. 2; Chap. X111; Sec. IV. This result was based on a description of
on a two-dimensional complex projective manifold, the Kawamata–Viehweg vanishing theorem was well known as the Picard theorem on the regularity of the adjoint, [a13], Vol. 2; Chap. X111; Sec. IV. This result was based on a description of  [a9], Formula I.17, in terms of the double point divisor of a sufficiently general projection of
[a9], Formula I.17, in terms of the double point divisor of a sufficiently general projection of  into
into  .
.
The next large step towards the Kawamata–Viehweg vanishing theorem was due to K. Kodaira [a10]. By means of a curvature technique that S. Bochner [a2] had used to show vanishing of real cohomology groups, Kodaira showed that for an ample line bundle  on a compact complex projective manifold,
on a compact complex projective manifold, 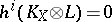 for
for 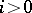 . Many generalizations of the Kodaira vanishing theorem appeared. Especially notable are results of C.P. Ramanujan [a14], which include the Kawamata–Viehweg vanishing theorem in the two-dimensional case; see also [a12].
. Many generalizations of the Kodaira vanishing theorem appeared. Especially notable are results of C.P. Ramanujan [a14], which include the Kawamata–Viehweg vanishing theorem in the two-dimensional case; see also [a12].
The following formulation [a6], [a7], [a4] of the Kawamata–Viehweg vanishing theorem is better adapted to applications. To state it in its simplest form, additive notation is used and 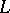 is taken to be a line bundle such that
is taken to be a line bundle such that 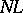 , i.e., the
, i.e., the 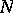 -th tensor power of
-th tensor power of 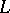 , can be written as a sum
, can be written as a sum  of a nef and big line bundle
of a nef and big line bundle  plus an effective divisor (cf. Divisor)
plus an effective divisor (cf. Divisor) 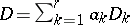 , where
, where  are positive integers and
are positive integers and 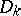 are smooth irreducible divisors such that any subset of the divisors meet transversely along their intersection. Then, for
are smooth irreducible divisors such that any subset of the divisors meet transversely along their intersection. Then, for  ,
,
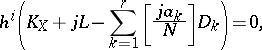 |
where  denotes the greatest integer less than or equal to a real number
denotes the greatest integer less than or equal to a real number  .
.
For more history and amplifications of these theorems see [a5], [a16]. See [a8] and [a11] for further generalizations of the Kawamata–Viehweg vanishing theorem. The paper [a8] is particularly useful: it contains relative versions of the vanishing theorem with some singularities, for not necessarily Cartier divisors. For applications of the vanishing theorems to classical problems, see [a1].
References
| [a1] | M. Beltrametti, A.J. Sommese, "The adjunction theory of complex projective varieties" , Experim. Math. , 16 , W. de Gruyter (1995) |
| [a2] | S. Bochner, "Curvature and Betti numbers I–II" Ann. of Math. , 49/50 (1948/9) pp. 379–390; 77–93 |
| [a3] | G. Castelnuovo, F. Enriques, "Sur quelques résultat nouveaux dans la théorie des surfaces algébriques" E. Picard (ed.) G. Simart (ed.) , Théorie des Fonctions Algébriques , I–II |
| [a4] | E. Viehweg, "Vanishing theorems" J. Reine Angew. Math. , 335 (1982) pp. 1–8 |
| [a5] | H. Esnault, E. Viehweg, "Lectures on vanishing theorems" , DMV-Sem. , 20 , Birkhäuser (1992) |
| [a6] | Y. Kawamata, "On the cohomology of 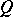 -divisors" Proc. Japan Acad. Ser. A , 56 (1980) pp. 34–35 -divisors" Proc. Japan Acad. Ser. A , 56 (1980) pp. 34–35 |
| [a7] | Y. Kawamata, "A generalization of Kodaira–Ramanujam's vanishing theorem" Math. Ann. , 261 (1982) pp. 43–46 |
| [a8] | Y. Kawamata, K. Matsuda, K. Matsuki, "Introduction to the minimal model problem" , Algebraic Geometry, Sendai 1985 , Adv. Stud. Pure Math. , 10 (1987) pp. 283–360 MR0946243 Zbl 0672.14006 |
| [a9] | S.L. Kleiman, "The enumerative theory of singularities" P. Holme (ed.) , Real and Complex Singularities, Oslo 1976 , Sijthoff&Noordhoff (1977) pp. 297–396 |
| [a10] | K. Kodaira, "On a differential-geometric method in the theory of analytic stacks" Proc. Nat. Acad. Sci. USA , 39 (1953) pp. 1268–1273 |
| [a11] | J. Kollár, "Higher direct images of dualizing sheaves I–II" Ann. of Math. , 123/4 (1986) pp. 11–42; 171–202 |
| [a12] | Y. Miyaoka, "On the Mumford–Ramanujam vanishing theorem on a surface" , Journees de Geometrie Algebrique, Angers/France 1979 (1980) pp. 239–247 |
| [a13] | Picard, G. Simart, "Théorie des fonctions algébriques I–II" , Chelsea, reprint (1971) |
| [a14] | C.P. Ramanujam, "Remarks on the Kodaira vanishing theorem" J. Indian Math. Soc. , 36 (1972) pp. 41–51 (See also the Supplement: J. Indian Math. Soc. 38 (1974), 121-124) |
| [a15] | G. Roch, "Über die Anzahl der willkürlichen Constanten in algebraischen Funktionen" J. de Crelle , 44 (1864) pp. 207–218 |
| [a16] | B. Shiffman, A.J. Sommese, "Vanishing theorems on complex manifolds" , Progr. Math. , 56 , Birkhäuser (1985) |
Kawamata-Viehweg vanishing theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kawamata-Viehweg_vanishing_theorem&oldid=23875