Difference between revisions of "Jacobson-Bourbaki theorem"
m (link) |
(Tex partly done) |
||
| Line 1: | Line 1: | ||
The Jacobson–Bourbaki theorem is especially useful for generalizations of the Galois theory of finite, normal and separable field extensions. | The Jacobson–Bourbaki theorem is especially useful for generalizations of the Galois theory of finite, normal and separable field extensions. | ||
| − | Let | + | Let $G$ be a [[finite group]] of automorphisms of a [[field]] $P$, and let $F$ be the subfield of elements of $P$ that are invariant under the action of $G$. Then $P$ is a normal and separable extension of $F$ (cf. [[Extension of a field]]), and there is a one-to-one correspondence between the subfields of $P$ containing $F$ and the subgroups of $G$ (cf. also [[Galois theory]]). The elements of $G$ are linear operators on the [[vector space]] $P$ over $F$; by the operation of multiplication, the elements of $P$ can be represented as linear operators on $P$ over $F$ (the [[Regular representation|regular representation]]), and the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001017.png" /> of all linear operators on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001018.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001019.png" /> is generated by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001020.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001021.png" />; indeed, it is the [[Cross product|cross product]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001022.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001023.png" />. |
Now, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001024.png" /> be a subfield of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001025.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001026.png" /> is a finite-dimensional vector space over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001027.png" /> and to each subfield <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001028.png" /> containing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001029.png" /> let correspond the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001030.png" /> of linear operators on the vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001031.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001032.png" />. The Jacobson–Bourbaki theorem asserts that this correspondence is a [[Bijection|bijection]] between the subfields of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001033.png" /> containing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001034.png" /> and the set of subrings of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001035.png" /> that are left vector spaces over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001036.png" /> of finite dimension. Moreover, the dimension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001037.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001038.png" /> equals the dimension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001039.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001040.png" />. | Now, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001024.png" /> be a subfield of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001025.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001026.png" /> is a finite-dimensional vector space over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001027.png" /> and to each subfield <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001028.png" /> containing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001029.png" /> let correspond the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001030.png" /> of linear operators on the vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001031.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001032.png" />. The Jacobson–Bourbaki theorem asserts that this correspondence is a [[Bijection|bijection]] between the subfields of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001033.png" /> containing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001034.png" /> and the set of subrings of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001035.png" /> that are left vector spaces over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001036.png" /> of finite dimension. Moreover, the dimension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001037.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001038.png" /> equals the dimension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001039.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j110/j110010/j11001040.png" />. | ||
| Line 11: | Line 11: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N. Jacobson, "Galois theory of purely inseparable fields of exponent one" ''Amer. J. Math.'' , '''66''' (1944) pp. 645–648</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N. Jacobson, "Galois theory of purely inseparable fields of exponent one" ''Amer. J. Math.'' , '''66''' (1944) pp. 645–648</TD></TR></table> | ||
| + | |||
| + | |||
| + | {{TEX|part}} | ||
Revision as of 18:33, 7 November 2016
The Jacobson–Bourbaki theorem is especially useful for generalizations of the Galois theory of finite, normal and separable field extensions.
Let $G$ be a finite group of automorphisms of a field $P$, and let $F$ be the subfield of elements of $P$ that are invariant under the action of $G$. Then $P$ is a normal and separable extension of $F$ (cf. Extension of a field), and there is a one-to-one correspondence between the subfields of $P$ containing $F$ and the subgroups of $G$ (cf. also Galois theory). The elements of $G$ are linear operators on the vector space $P$ over $F$; by the operation of multiplication, the elements of $P$ can be represented as linear operators on $P$ over $F$ (the regular representation), and the ring 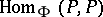 of all linear operators on
of all linear operators on  over
over  is generated by
is generated by  and
and 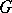 ; indeed, it is the cross product of
; indeed, it is the cross product of 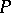 and
and 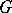 .
.
Now, let 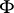 be a subfield of
be a subfield of 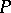 such that
such that 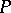 is a finite-dimensional vector space over
is a finite-dimensional vector space over 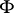 and to each subfield
and to each subfield 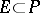 containing
containing 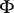 let correspond the ring
let correspond the ring 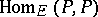 of linear operators on the vector space
of linear operators on the vector space 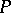 over
over 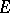 . The Jacobson–Bourbaki theorem asserts that this correspondence is a bijection between the subfields of
. The Jacobson–Bourbaki theorem asserts that this correspondence is a bijection between the subfields of 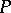 containing
containing 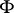 and the set of subrings of
and the set of subrings of 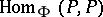 that are left vector spaces over
that are left vector spaces over 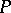 of finite dimension. Moreover, the dimension of
of finite dimension. Moreover, the dimension of 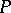 over
over 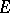 equals the dimension of
equals the dimension of 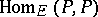 over
over 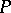 .
.
This theorem has been used by N. Jacobson to develop a Galois theory of finite, purely inseparable field extensions of exponent one, in which groups of automorphisms are replaced by Lie algebras of derivations, [a1].
The Jacobson–Bourbaki theorem can be regarded as an instance of Morita duality. From the theory of Morita equivalence the following very general result is obtained. Let 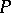 be a ring, let
be a ring, let 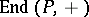 be the ring of endomorphisms of the additive group of
be the ring of endomorphisms of the additive group of 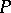 an note that
an note that 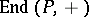 is a left module over
is a left module over 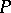 . There is a one-to-one correspondence between those subrings
. There is a one-to-one correspondence between those subrings 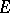 of
of 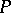 such that
such that 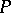 is a finitely generated projective generator in the category of right
is a finitely generated projective generator in the category of right 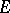 -modules and the subrings
-modules and the subrings 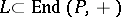 such that
such that 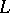 is a submodule of the left
is a submodule of the left 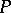 -module
-module 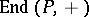 and
and 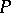 is a finitely generated projective generator in the category of left
is a finitely generated projective generator in the category of left 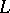 -modules.
-modules.
References
| [a1] | N. Jacobson, "Galois theory of purely inseparable fields of exponent one" Amer. J. Math. , 66 (1944) pp. 645–648 |
Jacobson-Bourbaki theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jacobson-Bourbaki_theorem&oldid=39690