Difference between revisions of "Jacobian conjecture"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 78 formulas out of 79 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 79 formulas, 78 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
''Keller problem'' | ''Keller problem'' | ||
| − | Let | + | Let $F = ( F _ { 1 } , \dots , F _ { n } ) : \mathbf{C} ^ { n } \rightarrow \mathbf{C} ^ { n }$ be a polynomial mapping, i.e. each $F_{i}$ is a polynomial in $n$ variables. If $F$ has a polynomial mapping as an inverse, then the chain rule implies that the [[Determinant|determinant]] of the [[Jacobi matrix|Jacobi matrix]] is a non-zero constant. In 1939, O.H. Keller asked: is the converse true?, i.e. does $\operatorname{det} JF \in \mathbf{C}^*$ imply that $F$ has a polynomial inverse?, [[#References|[a4]]]. This problem is now known as Keller's problem but is more often called the Jacobian conjecture. This conjecture is still open (1999) for all $n \geq 2$. Polynomial mappings satisfying $\operatorname{det} JF \in \mathbf{C}^*$ are called Keller mappings. Various special cases have been proved: |
| − | 1) if | + | 1) if $\operatorname { deg } F = \operatorname { max } _ { i } \operatorname { deg } F _ { i } \leq 2$, the conjecture holds (S.S. Wang). Furthermore, it suffices to prove the conjecture for all $n \geq 2$ and all Keller mappings of the form $( X _ { 1 } + H _ { 1 } , \dots , X _ { n } + H _ { n } )$ where each $H _ { i }$ is either zero or homogeneous of degree $3$ (H. Bass, E. Connell, D. Wright, A. Yagzhev). This case is referred to as the cubic homogeneous case. In fact, it even suffices to prove the conjecture for so-called cubic-linear mappings, i.e. cubic homogeneous mappings such that each $H _ { i }$ is of the form $l _ { i } ^ { 3 }$, where each $l_i$ is a linear form (L. Drużkowski). The cubic homogeneous case has been verified for $n \leq 4$ ($n = 3$ was settled by D. Wright; $n = 4$ was settled by E. Hubbers). |
| − | 2) A necessary condition for the Jacobian conjecture to hold for all | + | 2) A necessary condition for the Jacobian conjecture to hold for all $n \geq 2$ is that for Keller mappings of the form $F = X + F _ { ( 2 ) } + \ldots + F _ { ( d ) }$ with all non-zero coefficients in each $F_{ ( i )}$ positive, the mapping $F : \mathbf{R} ^ { n } \rightarrow \mathbf{R} ^ { n }$ is injective (cf. also [[Injection|Injection]]), where $F_{ ( i )}$ denotes the homogeneous part of degree $i$ of $F$. It is known that this condition is also sufficient! (J. Yu). On the other hand, the Jacobian conjecture holds for all $n \geq 2$ and all Keller mappings of the form $X + F _{( 2 )} + \ldots + F _{( d )}$, where each non-zero coefficient of all $F_{ ( i )}$ is negative (also J. Yu). |
| − | 3) The Jacobian conjecture has been verified under various additional assumptions. Namely, if | + | 3) The Jacobian conjecture has been verified under various additional assumptions. Namely, if $F$ has a rational inverse (O.H. Keller) and, more generally, if the field extension $\mathbf{C} ( F ) \subset \mathbf{C} ( X )$ is a [[Galois extension|Galois extension]] (L.A. Campbell). Also, properness of $F$ or, equivalently, if $\mathbf{C} [ X ]$ is finite over $\mathbf{C} [ F ]$ (cf. also [[Extension of a field|Extension of a field]]) implies that a Keller mapping is invertible. |
| − | 4) If | + | 4) If $n = 2$, the Jacobian conjecture has been verified for all Keller mappings $F$ with $\operatorname { deg } F \leq 100$ (T.T. Moh) and if $\operatorname { deg } F _ { 1 }$ or $\operatorname { deg } F _ { 2 }$ is a product of at most two prime numbers (H. Applegate, H. Onishi). Finally, if there exists one line $l \subset \mathbf{C} ^ { 2 }$ such that $F | _ { l } : l \rightarrow \mathbf{C} ^ { 2 }$ is injective, then a Keller mapping $F$ is invertible (J. Gwozdziewicz). There are various seemingly unrelated formulations of the Jacobian conjecture. For example, |
| − | a) up to a polynomial coordinate change, | + | a) up to a polynomial coordinate change, $( \partial _ { 1 } , \dots , \partial _ { n } )$ is the only commutative $\mathbf{C} [ X ]$-basis of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j120/j120010/j12001045.png"/>; |
| − | b) every order-preserving | + | b) every order-preserving $\mathbf{C}$-endomorphism of the $n$th [[Weyl algebra|Weyl algebra]] $A _ { n }$ is an isomorphism (A. van den Essen). |
| − | c) for every | + | c) for every $d , n \geq 1$ there exists a constant $C ( n , d ) > 0$ such that for every commutative $\mathbf{Q}$-algebra $R$ and every $F \in \operatorname { Aut } _ { R } R [ X ]$ with $\operatorname { det } J F = 1$ and $\operatorname { deg } F \leq d$, one has $\operatorname { deg } F ^ { - 1 } \leq C ( n , d )$ (H. Bass). |
| − | d) if | + | d) if $F : \mathbf{C} ^ { n } \rightarrow \mathbf{C} ^ { n }$ is a polynomial mapping such that $F ^ { \prime } ( z ) = \operatorname { det } J F ( z ) = 0$ for some $z \in \mathbf{C} ^ { n }$, then $F ( a ) = F ( b )$ for some $a \neq b \in {\bf C} ^ { n }$. |
| − | e) if, in the last formulation, one replaces | + | e) if, in the last formulation, one replaces $\mathbf{C}$ by $\mathbf{R}$ the so-called real Jacobian conjecture is obtained, i.e. if $F : \mathbf{R} ^ { n } \rightarrow \mathbf{R} ^ { n }$ is a polynomial mapping such that $\operatorname { det } J F ( x ) \neq 0$ for all $x \in \mathbf{R} ^ { n }$, then $F$ is injective. It was shown in 1994 (S. Pinchuk) that this conjecture is false for $n \geq 2$. Another conjecture, formulated by L. Markus and H. Yamabe in 1960 is the global asymptotic stability Jacobian conjecture, also called the Markus–Yamabe conjecture. It asserts that if $F : \mathbf{R} ^ { n } \rightarrow \mathbf{R} ^ { n }$ is a $C ^ { 1 }$-mapping with $F ( 0 ) = 0$ and such that for all $x \in \mathbf{R} ^ { n }$ the real parts of all eigenvalues of $J F ( x )$ are $< 0$, then each solution of $\dot { y } ( t ) = F ( y ( t ) )$ tends to zero if $t$ tends to infinity. The Markus–Yamabe conjecture (for all $n$) implies the Jacobian conjecture. For $n = 2$ the Markus–Yamabe conjecture was proved to be true (R. Fessler, C. Gutierrez). However, in 1995 polynomial counterexamples where found for all $n \geq 3$ (A. Cima, A. van den Essen, A. Gasull, E. Hubbers, F. Mañosas). |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> A. van den Essen, "Polynomial automorphisms and the Jacobian conjecture" J. Alev (ed.) et al. (ed.) , ''Algèbre Noncommutative, Groupes Quantiques et Invariants'' , SMF (1985) pp. 55–81</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> A. van den Essen, "Seven lectures on polynomial automorphisms" A. van den Essen (ed.) , ''Automorphisms of Affine Spaces'' , Kluwer Acad. Publ. (1995) pp. 3–39</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> H. Bass, E.H. Connell, D. Wright, "The Jacobian conjecture: reduction of degree and formal expansion of the inverse" ''Bull. Amer. Math. Soc.'' , '''7''' (1982) pp. 287–330</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> O.H. Keller, "Ganze Cremonatransformationen" ''Monatschr. Math. Phys.'' , '''47''' (1939) pp. 229–306</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> A. van den Essen, "Polynomial automorphisms and the Jacobian conjecture" , Birkhäuser (to appear in 2000)</td></tr></table> |
Revision as of 16:55, 1 July 2020
Keller problem
Let $F = ( F _ { 1 } , \dots , F _ { n } ) : \mathbf{C} ^ { n } \rightarrow \mathbf{C} ^ { n }$ be a polynomial mapping, i.e. each $F_{i}$ is a polynomial in $n$ variables. If $F$ has a polynomial mapping as an inverse, then the chain rule implies that the determinant of the Jacobi matrix is a non-zero constant. In 1939, O.H. Keller asked: is the converse true?, i.e. does $\operatorname{det} JF \in \mathbf{C}^*$ imply that $F$ has a polynomial inverse?, [a4]. This problem is now known as Keller's problem but is more often called the Jacobian conjecture. This conjecture is still open (1999) for all $n \geq 2$. Polynomial mappings satisfying $\operatorname{det} JF \in \mathbf{C}^*$ are called Keller mappings. Various special cases have been proved:
1) if $\operatorname { deg } F = \operatorname { max } _ { i } \operatorname { deg } F _ { i } \leq 2$, the conjecture holds (S.S. Wang). Furthermore, it suffices to prove the conjecture for all $n \geq 2$ and all Keller mappings of the form $( X _ { 1 } + H _ { 1 } , \dots , X _ { n } + H _ { n } )$ where each $H _ { i }$ is either zero or homogeneous of degree $3$ (H. Bass, E. Connell, D. Wright, A. Yagzhev). This case is referred to as the cubic homogeneous case. In fact, it even suffices to prove the conjecture for so-called cubic-linear mappings, i.e. cubic homogeneous mappings such that each $H _ { i }$ is of the form $l _ { i } ^ { 3 }$, where each $l_i$ is a linear form (L. Drużkowski). The cubic homogeneous case has been verified for $n \leq 4$ ($n = 3$ was settled by D. Wright; $n = 4$ was settled by E. Hubbers).
2) A necessary condition for the Jacobian conjecture to hold for all $n \geq 2$ is that for Keller mappings of the form $F = X + F _ { ( 2 ) } + \ldots + F _ { ( d ) }$ with all non-zero coefficients in each $F_{ ( i )}$ positive, the mapping $F : \mathbf{R} ^ { n } \rightarrow \mathbf{R} ^ { n }$ is injective (cf. also Injection), where $F_{ ( i )}$ denotes the homogeneous part of degree $i$ of $F$. It is known that this condition is also sufficient! (J. Yu). On the other hand, the Jacobian conjecture holds for all $n \geq 2$ and all Keller mappings of the form $X + F _{( 2 )} + \ldots + F _{( d )}$, where each non-zero coefficient of all $F_{ ( i )}$ is negative (also J. Yu).
3) The Jacobian conjecture has been verified under various additional assumptions. Namely, if $F$ has a rational inverse (O.H. Keller) and, more generally, if the field extension $\mathbf{C} ( F ) \subset \mathbf{C} ( X )$ is a Galois extension (L.A. Campbell). Also, properness of $F$ or, equivalently, if $\mathbf{C} [ X ]$ is finite over $\mathbf{C} [ F ]$ (cf. also Extension of a field) implies that a Keller mapping is invertible.
4) If $n = 2$, the Jacobian conjecture has been verified for all Keller mappings $F$ with $\operatorname { deg } F \leq 100$ (T.T. Moh) and if $\operatorname { deg } F _ { 1 }$ or $\operatorname { deg } F _ { 2 }$ is a product of at most two prime numbers (H. Applegate, H. Onishi). Finally, if there exists one line $l \subset \mathbf{C} ^ { 2 }$ such that $F | _ { l } : l \rightarrow \mathbf{C} ^ { 2 }$ is injective, then a Keller mapping $F$ is invertible (J. Gwozdziewicz). There are various seemingly unrelated formulations of the Jacobian conjecture. For example,
a) up to a polynomial coordinate change, $( \partial _ { 1 } , \dots , \partial _ { n } )$ is the only commutative $\mathbf{C} [ X ]$-basis of 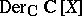 ;
;
b) every order-preserving $\mathbf{C}$-endomorphism of the $n$th Weyl algebra $A _ { n }$ is an isomorphism (A. van den Essen).
c) for every $d , n \geq 1$ there exists a constant $C ( n , d ) > 0$ such that for every commutative $\mathbf{Q}$-algebra $R$ and every $F \in \operatorname { Aut } _ { R } R [ X ]$ with $\operatorname { det } J F = 1$ and $\operatorname { deg } F \leq d$, one has $\operatorname { deg } F ^ { - 1 } \leq C ( n , d )$ (H. Bass).
d) if $F : \mathbf{C} ^ { n } \rightarrow \mathbf{C} ^ { n }$ is a polynomial mapping such that $F ^ { \prime } ( z ) = \operatorname { det } J F ( z ) = 0$ for some $z \in \mathbf{C} ^ { n }$, then $F ( a ) = F ( b )$ for some $a \neq b \in {\bf C} ^ { n }$.
e) if, in the last formulation, one replaces $\mathbf{C}$ by $\mathbf{R}$ the so-called real Jacobian conjecture is obtained, i.e. if $F : \mathbf{R} ^ { n } \rightarrow \mathbf{R} ^ { n }$ is a polynomial mapping such that $\operatorname { det } J F ( x ) \neq 0$ for all $x \in \mathbf{R} ^ { n }$, then $F$ is injective. It was shown in 1994 (S. Pinchuk) that this conjecture is false for $n \geq 2$. Another conjecture, formulated by L. Markus and H. Yamabe in 1960 is the global asymptotic stability Jacobian conjecture, also called the Markus–Yamabe conjecture. It asserts that if $F : \mathbf{R} ^ { n } \rightarrow \mathbf{R} ^ { n }$ is a $C ^ { 1 }$-mapping with $F ( 0 ) = 0$ and such that for all $x \in \mathbf{R} ^ { n }$ the real parts of all eigenvalues of $J F ( x )$ are $< 0$, then each solution of $\dot { y } ( t ) = F ( y ( t ) )$ tends to zero if $t$ tends to infinity. The Markus–Yamabe conjecture (for all $n$) implies the Jacobian conjecture. For $n = 2$ the Markus–Yamabe conjecture was proved to be true (R. Fessler, C. Gutierrez). However, in 1995 polynomial counterexamples where found for all $n \geq 3$ (A. Cima, A. van den Essen, A. Gasull, E. Hubbers, F. Mañosas).
References
| [a1] | A. van den Essen, "Polynomial automorphisms and the Jacobian conjecture" J. Alev (ed.) et al. (ed.) , Algèbre Noncommutative, Groupes Quantiques et Invariants , SMF (1985) pp. 55–81 |
| [a2] | A. van den Essen, "Seven lectures on polynomial automorphisms" A. van den Essen (ed.) , Automorphisms of Affine Spaces , Kluwer Acad. Publ. (1995) pp. 3–39 |
| [a3] | H. Bass, E.H. Connell, D. Wright, "The Jacobian conjecture: reduction of degree and formal expansion of the inverse" Bull. Amer. Math. Soc. , 7 (1982) pp. 287–330 |
| [a4] | O.H. Keller, "Ganze Cremonatransformationen" Monatschr. Math. Phys. , 47 (1939) pp. 229–306 |
| [a5] | A. van den Essen, "Polynomial automorphisms and the Jacobian conjecture" , Birkhäuser (to appear in 2000) |
Jacobian conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jacobian_conjecture&oldid=19054