Iwasawa decomposition
The unique representation of an arbitrary element  of a non-compact connected semi-simple real Lie group
of a non-compact connected semi-simple real Lie group  as a product
as a product  of elements
of elements 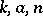 of analytic subgroups
of analytic subgroups 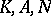 , respectively, where
, respectively, where  ,
,  and
and  are defined as follows. Let
are defined as follows. Let 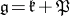 be a Cartan decomposition of the Lie algebra
be a Cartan decomposition of the Lie algebra 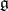 of
of 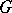 ; let
; let  be the maximal commutative subspace of the space
be the maximal commutative subspace of the space 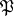 , and let
, and let 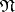 be a nilpotent Lie subalgebra of
be a nilpotent Lie subalgebra of 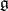 such that
such that 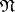 is the linear hull of the root vectors in some system of positive roots with respect to
is the linear hull of the root vectors in some system of positive roots with respect to  . The decomposition of the Lie algebra as the direct sum of the subalgebras
. The decomposition of the Lie algebra as the direct sum of the subalgebras 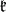 ,
,  and
and 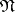 is called the Iwasawa decomposition [1] of the semi-simple real Lie algebra
is called the Iwasawa decomposition [1] of the semi-simple real Lie algebra 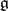 . The groups
. The groups  ,
, 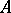 and
and 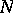 are defined to be the analytic subgroups of
are defined to be the analytic subgroups of 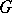 corresponding to the subalgebras
corresponding to the subalgebras 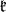 ,
,  and
and 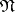 , respectively. The groups
, respectively. The groups 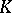 ,
,  and
and 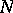 are closed;
are closed; 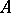 and
and 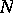 are simply-connected;
are simply-connected; 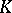 contains the centre of
contains the centre of 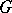 , and the image of
, and the image of 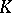 under the adjoint representation of
under the adjoint representation of 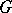 is a maximal compact subgroup of the adjoint group of
is a maximal compact subgroup of the adjoint group of 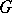 . The mapping
. The mapping 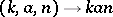 is an analytic diffeomorphism of the manifold
is an analytic diffeomorphism of the manifold 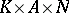 onto the Lie group
onto the Lie group 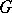 . The Iwasawa decomposition plays a fundamental part in the representation theory of semi-simple Lie groups. The Iwasawa decomposition can be defined also for connected semi-simple algebraic groups over a
. The Iwasawa decomposition plays a fundamental part in the representation theory of semi-simple Lie groups. The Iwasawa decomposition can be defined also for connected semi-simple algebraic groups over a  -adic field (or, more generally, for groups of
-adic field (or, more generally, for groups of 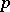 -adic type) (see [4], [5]).
-adic type) (see [4], [5]).
References
| [1] | K. Iwasawa, "On some types of topological groups" Ann. of Math. , 50 (1949) pp. 507–558 MR0029911 Zbl 0034.01803 |
| [2] | M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian) MR0793377 Zbl 0484.22018 |
| [3] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) MR0514561 Zbl 0451.53038 |
| [4] | F. Bruhat, "Sur une classe de sous-groupes compacts maximaux des groupes de Chevalley sur un corps 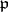 -adique" Publ. Math. IHES , 23 (1964) pp. 45–74 MR179298 -adique" Publ. Math. IHES , 23 (1964) pp. 45–74 MR179298 |
| [5] | N. Iwahori, H. Matsumoto, "On some Bruhat decomposition and the structure of the Hecke rings of 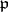 -adic Chevalley groups" Publ. Math. IHES , 25 (1965) pp. 5–48 MR185016 -adic Chevalley groups" Publ. Math. IHES , 25 (1965) pp. 5–48 MR185016 |
Comments
An example of an Iwasawa decomposition is 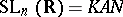 with
with 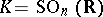 ,
, 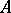 the subgroup of diagonal matrices of
the subgroup of diagonal matrices of 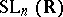 and
and 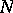 a lower triangular matrix with
a lower triangular matrix with 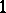 's on the diagonal. So, in particular, every element of
's on the diagonal. So, in particular, every element of 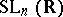 gets written as a product of a special orthogonal matrix and a lower triangular matrix.
gets written as a product of a special orthogonal matrix and a lower triangular matrix.
References
| [a1] | S. Helgason, "Groups and geometric analysis" , Acad. Press (1984) pp. Chapt. II, Sect. 4 MR0754767 Zbl 0543.58001 |
Iwasawa decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Iwasawa_decomposition&oldid=21877