Iversen theorem
From Encyclopedia of Mathematics
If  is an isolated essential singularity of an analytic function
is an isolated essential singularity of an analytic function 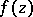 of a complex variable
of a complex variable  , then every exceptional value
, then every exceptional value 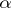 in the sense of E. Picard is an asymptotic value of
in the sense of E. Picard is an asymptotic value of 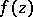 at
at  . For example, the values
. For example, the values 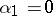 and
and  are exceptional and asymptotic values of
are exceptional and asymptotic values of 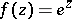 at the essential singularity
at the essential singularity 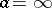 . This result of F. Iversen [1] supplements the big Picard theorem on the behaviour of an analytic function in a neighbourhood of an essential singularity.
. This result of F. Iversen [1] supplements the big Picard theorem on the behaviour of an analytic function in a neighbourhood of an essential singularity.
References
| [1] | F. Iversen, "Récherches sur les fonctions inverses des fonctions méromorphes" , Helsinki (1914) |
| [2] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 1;6 |
Comments
Iversen's theorem has been extended to subharmonic functions on 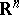 , notably by W.K. Hayman, see [a1], [a2].
, notably by W.K. Hayman, see [a1], [a2].
References
| [a1] | W.K. Hayman, P.B. Kennedy, "Subharmonic functions" , 1 , Acad. Press (1976) |
| [a2] | W.K. Hayman, "Subharmonic functions" , 2 , Acad. Press (1989) |
How to Cite This Entry:
Iversen theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Iversen_theorem&oldid=12397
Iversen theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Iversen_theorem&oldid=12397
This article was adapted from an original article by E.D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article