Itô process
$\newcommand{\Prob}{\mathsf{P}}$ $\newcommand{\Ex}{\mathsf{E}}$
A stochastic process with a stochastic differential. More precisely, a continuous stochastic process $X_t$ on a probability space $(\Omega, \mathcal{F}, \Prob)$ with a certain non-decreasing family $\{\mathcal F_t\}$ of $\sigma$-algebras of  is called an Itô process with respect to
is called an Itô process with respect to 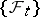 if there exists processes
if there exists processes 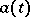 and
and 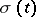 (called the drift coefficient and the diffusion coefficient, respectively), measurable with respect to
(called the drift coefficient and the diffusion coefficient, respectively), measurable with respect to 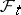 for each
for each  , and a Wiener process
, and a Wiener process 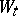 with respect to
with respect to 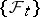 , such that
, such that
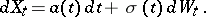 |
Such processes are called after K. Itô [1], [2]. One and the same process 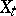 can be an Itô process with respect to two different families
can be an Itô process with respect to two different families 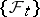 . The corresponding stochastic differentials may differ substantially in this case. An Itô process is called a process of diffusion type (cf. also Diffusion process) if its drift coefficient
. The corresponding stochastic differentials may differ substantially in this case. An Itô process is called a process of diffusion type (cf. also Diffusion process) if its drift coefficient 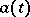 and diffusion coefficient
and diffusion coefficient 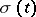 are, for each
are, for each 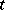 , measurable with respect to the
, measurable with respect to the 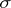 -algebra
-algebra
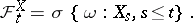 |
Under certain, sufficiently general, conditions it is possible to represent an Itô process as a process of diffusion type, but, generally, with some new Wiener process (cf. [3]). If an Itô process 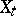 is representable as a diffusion Itô process with some Wiener process
is representable as a diffusion Itô process with some Wiener process 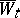 and if the equation
and if the equation 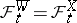 is satisfied, then
is satisfied, then 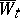 is called the innovation process for
is called the innovation process for 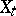 .
.
Examples. Suppose that a certain Wiener process 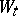 ,
, 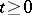 , with respect to
, with respect to 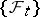 has been given and suppose that
has been given and suppose that
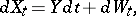 |
where 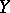 is a normally-distributed random variable with mean
is a normally-distributed random variable with mean 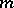 and variance
and variance 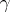 that is measurable with respect to
that is measurable with respect to 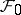 .
.
The process 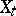 , regarded with respect to
, regarded with respect to 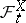 , has stochastic differential
, has stochastic differential
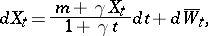 |
in which the new Wiener process 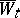 , defined by
, defined by
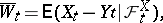 |
is an innovation process for 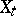 .
.
References
| [1] | I.V. Girsanov, "Transforming a certain class of stochastic processes by absolutely continuous substitution of measures" Theor. Probab. Appl. , 5 : 3 (1960) pp. 285–301 Teor. Veroyatnost. i Primenen. , 5 : 3 (1960) pp. 314–330 |
| [2] | R.S. Liptser, A.N. Shiryaev, "Statistics of random processes" , 1–2 , Springer (1977–1978) (Translated from Russian) |
| [3] | A.N. Shiryaev, "Stochastic equations of nonlinear filtering of Markovian jump processes" Probl. Inform. Transmission , 2 : 3 (1966) pp. 1–8 Probl. Peredachi Inform. , 2 : 3 (1966) pp. 3–22 |
Comments
For additional references see Itô formula.
Itô process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=It%C3%B4_process&oldid=35534