Isotropy group
The set  of elements of a given group
of elements of a given group  , acting on a set
, acting on a set  as a group of transformations, that leave a point
as a group of transformations, that leave a point  fixed. This set turns out to be a subgroup of
fixed. This set turns out to be a subgroup of  and is called the isotropy group of the point
and is called the isotropy group of the point  . The following terminology is used with the same meaning: stationary subgroup, stabilizer,
. The following terminology is used with the same meaning: stationary subgroup, stabilizer,  -centralizer. If
-centralizer. If  is a Hausdorff space and
is a Hausdorff space and 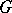 is a topological group acting continuously on
is a topological group acting continuously on 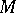 , then
, then 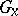 is a closed subgroup. If, furthermore,
is a closed subgroup. If, furthermore,  and
and  are locally compact,
are locally compact, 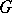 has a countable base and acts transitively on
has a countable base and acts transitively on 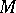 , then there exists a unique homeomorphism from
, then there exists a unique homeomorphism from 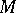 into the quotient space
into the quotient space 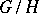 , where
, where  is one of the isotropy groups; all the
is one of the isotropy groups; all the 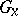 ,
,  , are isomorphic to
, are isomorphic to 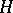 .
.
Let 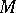 be a smooth manifold and
be a smooth manifold and 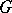 a Lie group acting smoothly on
a Lie group acting smoothly on 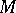 . Then the isotropy group
. Then the isotropy group 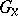 of a point
of a point 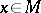 induces a group of linear transformations of the tangent vector space
induces a group of linear transformations of the tangent vector space 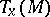 ; the latter is called the linear isotropy group at
; the latter is called the linear isotropy group at  . On passing to tangent spaces of higher order at the point
. On passing to tangent spaces of higher order at the point  one obtains natural representations of the isotropy group in the structure groups of the corresponding tangent bundles of higher order; they are called the higher-order isotropy groups (see also Isotropy representation).
one obtains natural representations of the isotropy group in the structure groups of the corresponding tangent bundles of higher order; they are called the higher-order isotropy groups (see also Isotropy representation).
References
| [1] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) |
| [2] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) |
| [3] | R. Sulanke, P. Wintgen, "Differentialgeometrie und Faserbündel" , Deutsch. Verlag Wissenschaft. (1972) |
Isotropy group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Isotropy_group&oldid=17780