Intuitionism
The set of philosophical and mathematical ideas and methods that regard mathematics as a science of mental construction. From the point of view of intuitionism, the basic criterion for truth of a mathematical reasoning is intuitive evidence of the possibility of performing a mental experiment related to this reasoning. Therefore, in intuitionistic mathematics one rejects the set-theoretic approach to the definition of mathematical concepts, as well as certain ways of reasoning customary in classical logic.
The source of intuitionism can already be traced in mathematics of Antiquity, and later in statements of scholars like C.F. Gauss, L. Kronecker, H. Poincaré, H. Lebesgue, and E. Borel. From 1907 onwards L.E.J. Brouwer advanced in a series of papers detailed criticism of certain conceptions in classical mathematics. At the basis of this criticism lies a consideration of the status of existence in mathematics: In what sense may one consider as established the existence of an actually given infinite set and the potential realizability of objects of research such as a non-measurable set of real numbers or a nowhere-differentiable function? It is natural to assume that one can construct an arbitrary natural number as a sequence of single-type objects, e.g. as a series of parallel strokes. Within the framework of the same idealization one may allow, after having constructed some natural number, the possibility of constructing the next, adding one more stroke to the already constructed. However, the question that arises is: With what kind of construction does one associate the set of all real numbers, or the set of natural numbers, as a single object of study? Modern physical conceptions do not give a good foundation for this, by stating that in the surrounding world there actually do exist infinite sets of objects. A more serious foundation is provided if one states that objects whose existence has been established without the use of the abstraction of actual infinity, but within the much more restricted abstraction of potential realizability, have a more direct relation to reality. However, in the ordinary set-theoretic treatment one does not distinguish between objects whose existence can be verified by a potentially realizable construction, and abstract set-theoretic objects of study. In classical mathematics methods of establishing properties of both objects are based on the laws of logic that arise as the result of extrapolating to infinite sets laws that hold for finite sets. In the region of the infinite these laws are not oriented towards an effective construction of the objects whose existence is stated. This approach led in fact to the appearance in mathematics of so-called "pure existence theorems" , in which the existence of certain objects is stated while at the same time no means is indicated for finding them. Such is, e.g., the classical theorem of analysis stating that every real-valued continuous function on a closed bounded set in 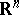 attains a maximum. The usual proof of this theorem does not give an indication of a method for constructing the required maximum. This does not disagree with set-theoretic mathematics: It can be considered that a maximum "exists" for every function in the class considered, independent of the question whether it can be found in each individual case or not; it "exists" as an object of some conceivable world (a "Platonic world" , cf. [6]). However, such an approach does not suffice if one takes the possibility of a subject-investigator into account. Is there a method for finding a maximum, and if such a method cannot be given, is it then true that a maximum exists for every function of the class considered? It is well-known how difficult it is to find an extremum for functions of a very restricted class (polynomials with rational coefficients in several variables), and, what is essential, the theorem indicated does not help at all in solving this problem. It should be noted that the above criticism of classical mathematics is not directly related to antinomies in set theory (cf. Antinomy). The appearance of antinomies can be regarded as a supplementary proof of the unsatisfactoriness of the set-theoretic approach, but this criticism is also directed towards branches of mathematics in which no antinomies appear.
attains a maximum. The usual proof of this theorem does not give an indication of a method for constructing the required maximum. This does not disagree with set-theoretic mathematics: It can be considered that a maximum "exists" for every function in the class considered, independent of the question whether it can be found in each individual case or not; it "exists" as an object of some conceivable world (a "Platonic world" , cf. [6]). However, such an approach does not suffice if one takes the possibility of a subject-investigator into account. Is there a method for finding a maximum, and if such a method cannot be given, is it then true that a maximum exists for every function of the class considered? It is well-known how difficult it is to find an extremum for functions of a very restricted class (polynomials with rational coefficients in several variables), and, what is essential, the theorem indicated does not help at all in solving this problem. It should be noted that the above criticism of classical mathematics is not directly related to antinomies in set theory (cf. Antinomy). The appearance of antinomies can be regarded as a supplementary proof of the unsatisfactoriness of the set-theoretic approach, but this criticism is also directed towards branches of mathematics in which no antinomies appear.
The criticism of the set-theoretic approach to mathematics, described above, historically led to the development of two ways to overcome the difficulties in the foundation of mathematics — Brouwer's intuitionism and D. Hilbert's formalism. After their elaboration, both conceptions now show a significant influence on one another. Thus, when substantiating the consistency of formal theories, it becomes necessary to make precise the means of useful inference in mathematics; this is usually done within some intuitionistic conception. On the other hand, by using the formalization method one can find a number of important results on the logic of intuitionism.
Intuitionistic mathematics is the science of intuitively-convincing mental constructions. Brouwer himself treated this intuitive persuasiveness as idealistic, by considering mental constructions as such, "irrespective of such questions on the nature of constructed objects, as the question of whether these objects exist independently of our knowledge about them" (cf. [1]). However, there is also a materialistic source of the "intuition" of intuitionism possible, as an explicit mental persuasiveness of the simplest constructive processes of real activity. Independently of the philosophical positions, the concrete mathematical results related to intuitionistic mathematics and logic are of great scientific value.
In the construction of intuitionistic mathematics, the ordinary logical connectives used in formulating mathematical assertions are interpreted in a way that differs from the classical way. An assertion is considered true only if the investigator has a means of proving it. The proof is always related here to performing some mental construction. Thus, a statement starting with the existential quantifier, 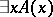 , can be proved only by constructing an object
, can be proved only by constructing an object  for which the assertion
for which the assertion 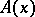 can be proved. The disjunction
can be proved. The disjunction 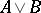 of two statements
of two statements 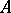 and
and 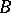 is considered as being proved only if the investigator has at his disposal a method for proving one of
is considered as being proved only if the investigator has at his disposal a method for proving one of 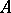 or
or 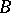 . From this point of view, a statement
. From this point of view, a statement 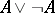 need not be true if one cannot indicate a method that will eventually yield a proof of either
need not be true if one cannot indicate a method that will eventually yield a proof of either 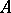 or
or 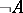 . Hence it is clear that the law of the excluded middle is not applicable in intuitionistic mathematics as a logical principle. A true mathematical statement is a message concerning constructions that can be performed, and the effective character of these constructions presupposes the use of a special intuitionistic logic different from classical logic. Effectivity is, moreover, to be regarded in a broad sense; it is not related to the existence of an algorithm in a precise sense of this word and may, e.g., have the character of a historical accumulation of facts, or may depend on an actual solution of a problem or on physical factors.
. Hence it is clear that the law of the excluded middle is not applicable in intuitionistic mathematics as a logical principle. A true mathematical statement is a message concerning constructions that can be performed, and the effective character of these constructions presupposes the use of a special intuitionistic logic different from classical logic. Effectivity is, moreover, to be regarded in a broad sense; it is not related to the existence of an algorithm in a precise sense of this word and may, e.g., have the character of a historical accumulation of facts, or may depend on an actual solution of a problem or on physical factors.
The objects of research in intuitionistic mathematics are first of all constructive objects such as the natural or rational numbers, and finite sets of constructive objects given by listing their elements (cf. Constructive object). Intrinsic objects of study are the so-called freely-established sequences (in another terminology: choice sequences). Choice sequences can be represented by functions defined on the natural numbers, taking as values the objects of research of a certain class (in the simplest case: natural numbers), and such that every value of it effectively becomes an admissible sequence. Exact analysis shows that one has to distinguish between several kinds of choice sequences, depending on the degree of information, known to the investigator, about the choice sequence. Thus, if the full law of forming the choice sequence is known, e.g. as a description of a corresponding algorithm, then such a choice sequence is called a lawlike sequence. The other extreme is that at each moment of time the investigator knows only an initial segment of the choice sequence, and has no information whatsoever on its future behaviour; such choice sequences are called lawless. This distinction, which is ignored in classical mathematics, can be expressed in intuitionistic mathematics by fine mathematical principles, reflecting the various ways of forming such choice sequences. Finally, so-called intuitionistic species may serve as objects of research in intuitionistic mathematics. A species is a property that objects of research can have. The objects with this property are called the elements, or terms, of the species. In order to avoid the appearance of antinomies, one can introduce a hierarchy among the species, analogous to the theory of types (cf. Types, theory of), by requiring that the elements of a species are defined independently of the definition of the species itself. It is clear that the extensive introduction of species in intuitionistic mathematics gives rise to problems (in intuitionistic mathematics) which are characteristic of abstract set theory, such as predicativity, the appearance of antinomies, etc. However, one must bear in mind that, on the one hand, dealing with species is very different from dealing with sets in classical mathematics, while, on the other hand, in practical work in intuitionistic mathematics species take an extremely modest place. In reality, an overwhelming number of the results can be formulated and proved without the use of species as independent objects of research at all. This is related to the natural trend in intuitionism to regard effectively-constructible or effectively-generated objects as objects of research. Other "non-traditional" objects of research are also being considered within the frame of intuitionism. It appears fruitful to study effective functionals of finite type. By using these, one can construct, within the frame of intuitionism, an interpretation of classical analysis (P.S. Novikov, K. Gödel, C. Spector).
The refusal to consider actually-given infinite sets, and the requirement of effectiveness of all realizable objects, lead to the fact that some branches of traditional mathematics acquire a very unusual form in intuitionism. The real line is not treated as a set of individual points, but as a "means of formation" , as a spread of refining rational intervals (cf. Spread (in intuitionistic logic)). Each individual intuitionistic real number determines a choice sequence, whose values are unboundedly-refining nested rational intervals. In arguments on the intuitionistic real line one uses specific principles such as bar induction and the fan theorem. A consequence of this is, e.g., that in the natural system of concepts every intuitionistic real-valued function defined on a closed segment is uniformly continuous. Intuitionistic mathematics is a well-developed direction in mathematics containing many deep results, including some in branches such as measure theory, functional analysis, topology, and the theory of differential equations.
Somewhat aside from this research stands the attempt of H. Weyl (1918) to construct mathematics on the basis of the predicative approach. Agreeing largely with the intuitionistic criticism, Weyl proposed that one should restrict oneself to constructive objects of research and specify sets as conditions in a certain language, defined in such a way that the predicativity of the definition of sets is not violated. Subsequently, Weyl joined the intuitionistic conception of the construction of mathematics, but his views laid the basis for deep research on the foundation of mathematics.
By considering the criterion of truth of a construction as first of all intuitive, and opposite to formalism, Brouwer was opposed to the attempts to formalize intuitionistic mathematics and, above all, intuitionistic logic. However, considerable success in the study of intuitionistic logic was achieved only after its basic laws were precisely formulated as a calculus, to which one may apply exact methods of mathematical logic. In the development of intuitionistic logic mathematicians not considering themselves "intuitionists" participated considerably. Moreover, the problem of "truth in intuitionism" became of secondary importance, and special intuitionistic calculi gained large pure mathematical interest because they clarified different ideas of effectiveness in mathematics. The modern direction of development of intuitionism is part of constructive mathematics in the widest sense of the latter term.
After the exact formulation, by A. Heyting, of intuitionistic predicate calculus (cf. Intuitionistic logic), a topological interpretation (A. Tarski) and an interpretation as a calculus of problems (A.N. Kolmogorov) were found. The independence of the logical connectives and the impossibility of representing intuitionistic predicate calculus as a finite-valued logic (K. Gödel) were proved. Heyting described intuitionistic arithmetical calculus, which is obtained if classical arithmetical calculus is considered on the basis of intuitionistic predicate calculus. For predicate and arithmetical calculus, Kolmogorov and Gödel advanced the immersion operation (or interpretation) of the classical calculus in the negative part of the corresponding intuitionistic calculus. This implies, in particular, the consistency of the classical calculus if the intuitionistic calculus is consistent. The intuitionistic disjunction and existence properties were established. These are: if the statement 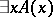 is deducible, then
is deducible, then 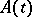 is deducible for some term
is deducible for some term  ; the deducibility of
; the deducibility of 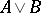 implies that of
implies that of 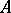 or that of
or that of 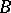 . Some variants of the intuitionistic concept of a statement were proposed by S.C. Kleene in the form of recursive realizability. It is precisely this sense that is characteristic for the constructive direction in mathematics as developed by the school of A.A. Markov in the USSR. Understanding the term "intuitionism" sufficiently broadly, one can regard the constructive direction in mathematics as a variant of intuitionism in which the study of constructive objects and constructive processes by algorithmic methods is characteristic.
. Some variants of the intuitionistic concept of a statement were proposed by S.C. Kleene in the form of recursive realizability. It is precisely this sense that is characteristic for the constructive direction in mathematics as developed by the school of A.A. Markov in the USSR. Understanding the term "intuitionism" sufficiently broadly, one can regard the constructive direction in mathematics as a variant of intuitionism in which the study of constructive objects and constructive processes by algorithmic methods is characteristic.
The problem of the semantic completeness of intuitionistic predicate calculus has been investigated. An exhaustive algebraic characterization of deducibility was given in theories of models of intuitionistic logic (by E. Beth and S. Kripke). These theories have applications in other parts of intuitionistic mathematics. Intuitionistic logic is complete with respect to certain conceptions of a choice sequence; however, it is not complete with respect to recursive realizability. The intuitionistic notion of quantifiers allows one to formulate in arithmetic the Church thesis as a mathematical statement. This can be done, e.g., in the form "If for every natural number x there is a natural number y satisfying a relation Ax, y, then there is a general recursive function f such that Ax, fx holds for every x" ; the relation 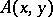 must not contain non-constructive parameters of the type of choice sequences. Markov's constructive selection principle can also naturally be formulated in the language of arithmetic. The relation between these two fundamental principles in intuitionistic theories is the subject of a number of contemporary studies.
must not contain non-constructive parameters of the type of choice sequences. Markov's constructive selection principle can also naturally be formulated in the language of arithmetic. The relation between these two fundamental principles in intuitionistic theories is the subject of a number of contemporary studies.
A satisfactory construction of the theory of choice sequences and higher branches of intuitionistic mathematics was completed in the 1970s. Usually, the language of the formal theory of intuitionistic analysis contains two kinds of variables: variables 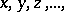 for natural numbers, and variables
for natural numbers, and variables 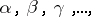 for choice sequences, mapping natural numbers to natural numbers. The theory contains as terms symbols for primitive-recursive operations on functions and numbers. The atomic formulas have the form of equality of two terms, quantifiers are used for both kinds of variable. The theory contains all postulates of intuitionistic arithmetical calculus. This group of postulates ensures the introduction of all basic properties of primitive-recursive transformations on functions and numbers. Thus, it is possible to describe in the theory a one-to-one method of encoding finite sequences (tuples, cf. Tuple) of natural numbers by natural numbers. Let
for choice sequences, mapping natural numbers to natural numbers. The theory contains as terms symbols for primitive-recursive operations on functions and numbers. The atomic formulas have the form of equality of two terms, quantifiers are used for both kinds of variable. The theory contains all postulates of intuitionistic arithmetical calculus. This group of postulates ensures the introduction of all basic properties of primitive-recursive transformations on functions and numbers. Thus, it is possible to describe in the theory a one-to-one method of encoding finite sequences (tuples, cf. Tuple) of natural numbers by natural numbers. Let  denote the number of the tuple with
denote the number of the tuple with  as terms;
as terms; 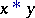 is the operation of concatenation of tuples, i.e. if
is the operation of concatenation of tuples, i.e. if 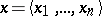 and
and 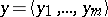 , then
, then 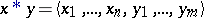 . The number of a tuple with one term,
. The number of a tuple with one term,  , is denoted by
, is denoted by 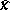 . Let
. Let 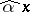 denote the tuple
denote the tuple  . One introduces the predicate "a is a continuous operator" by:
. One introduces the predicate "a is a continuous operator" by: 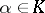 means
means
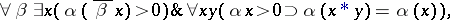 |
the results of applying a continuous operator to choice sequences are defined as follows: 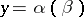 means
means
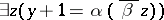 |
and  means
means
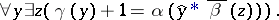 |
Further, let 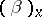 denote the function
denote the function 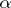 for which
for which
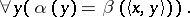 |
Using these operations, one can precisely formulate some fundamental principles, related, in particular, to choice sequences. First of all, there are the intuitionistic axiom of choice
 |
Brouwer's continuity principle
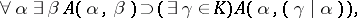 |
and bar induction. These principles give the formal theory of choice sequences, as proposed by Kleene. This theory is sufficient for obtaining all the basic theorems of intuitionistic analysis, including the fan theorem, the uniform continuity of a continuous function, etc. One must bear in mind that this theory reflects only one kind of intuitionistic sequence, the kind that is specially convenient for constructing intuitionistic analysis. Another characteristic kind of choice sequence is the lawless sequence mentioned above. The following principle of open data states that all information on a lawless sequence can be extracted by investigating its initial segments:
 |
Here 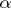 is the only choice-sequence variable occurring in
is the only choice-sequence variable occurring in 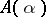 .
.
One more kind of choice sequence arises in the attempt to express in a formal theory the existence of choice sequences: those depending on the solution to a problem. For such choice sequences the so-called Kripke scheme holds:
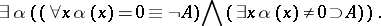 |
Different intuitionistic principles apply to the various kinds of choice sequences. Thus, for lawless sequences the intuitionistic axiom of choice in its general form does not hold, and for sequences depending on the solution to a problem Brouwer's continuity principle in the form indicated does not hold. Far-less developed is the formal theory for expressing the intuitionistic theory of types. However, here too there are attempts at formulating the specific intuitionistic means of dealing with types. E.g., if 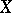 is a variable for types of natural numbers, then the following so-called uniformity principle [4] may be accepted:
is a variable for types of natural numbers, then the following so-called uniformity principle [4] may be accepted:
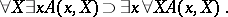 |
Until the second half of the 20th century the ideas of Brouwer were fully appreciated only by a narrow group of mathematicians, intuitionists, although they exerted great influence on all further research on the foundations of mathematics. More recently this has changed. The development of proof theory made it possible to formulate the basic intuitionistic theories in the form of exact calculi and to subject them to precise investigation. The development of the computational trend in mathematics aroused interest in the logical analysis of effective tools of proof and in the study of the abstractions used in mathematics. Various programs for rebuilding mathematics on the basis of some idea of constructivity arose. The synthesis of traditional methods of intuitionism with modern methods of proof theory made it possible to advance intuitionism considerably.
References
| [1] | A. Heyting, "Intuitionism: an introduction" , North-Holland (1970) |
| [2] | S.C. Kleene, R.E. Vesley, "The foundations of intuitionistic mathematics: especially in relation to recursive functions" , North-Holland (1965) |
| [3] | G. Kreisel, A.S. Troelstra, "Formal systems for some branches of intuitionistic analysis" Ann. Math. Logic , 1 : 3 (1970) pp. 229–387 |
| [4] | A.S. Troelstra (ed.) , Metamathematical investigation of intuitionistic arithmetic and analysis , Lect. notes in math. , 344 , Springer (1973) |
| [5] | P. Martin-Löf, "Notes on constructive mathematics" , Almqvist & Wiksell (1970) |
| [6] | A.A. Fraenkel, Y. Bar-Hillel, "Foundations of set theory" , North-Holland (1958) |
Comments
Another factor which has influenced the revival of interest in intuitionism, mentioned above, is the rise of categorical logic and in particular of the logical aspects of topos theory (see Topos). The internal logic of a topos is formally intuitionistic in character; indeed, a topos can be considered as a model of higher-order intuitionistic type theory, and topos models for intuitionism generalize both the algebraic models of Beth and Kripke and the topological models of Tarski and Scott.
A comprehensive up-to-date account is [a3], which also contains an extensive bibliography.
References
| [a1] | M.P. Fourman, "The logic of topoi" J. Barwise (ed.) , Handbook of mathematical logic , North-Holland (1977) pp. 1053–1090 |
| [a2] | M.P. Fourman, D.S. Scott, "Sheaves and logic" M.P. Fourman (ed.) C.J. Mulvey (ed.) D.S. Scott (ed.) , Applications of sheaves , Lect. notes in math. , 753 , Springer (1979) pp. 302–401 |
| [a3] | A.S. Troelstra, D. van Dalen, "Constructivism in mathematics, an introduction" , 1–2 , North-Holland (1989) |
| [a4] | M.A.E. Dummett, "Elements of intuitionism" , Oxford Univ. Press (1977) |
| [a5] | D. van Dalen (ed.) , Brouwer's Cambridge lectures on intuitionism , Cambridge Univ. Press (1981) |
| [a6] | M.J. Beeson, "Foundations of constructive mathematics" , Springer (1985) |
Intuitionism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Intuitionism&oldid=18352