Inner automorphism
of a group 
An automorphism  such that
such that
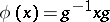 |
for a certain fixed element  . The set of all inner automorphisms of
. The set of all inner automorphisms of  forms a normal subgroup in the group of all automorphisms of
forms a normal subgroup in the group of all automorphisms of  ; this subgroup is isomorphic to
; this subgroup is isomorphic to  , where
, where  is the centre of
is the centre of  (cf. Centre of a group). Automorphisms that are not inner are called outer automorphisms.
(cf. Centre of a group). Automorphisms that are not inner are called outer automorphisms.
Other relevant concepts include those of an inner automorphism of a monoid (a semi-group with a unit element) and an inner automorphism of a ring (associative with a unit element), which are introduced in a similar way using invertible elements.
Comments
Let 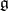 be a Lie algebra and
be a Lie algebra and  an element of
an element of  for which
for which 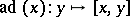 is nilpotent. Then
is nilpotent. Then
 |
defines an automorphism of 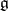 . Such an automorphism is called an inner automorphism of
. Such an automorphism is called an inner automorphism of 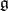 . More generally, the elements in the group
. More generally, the elements in the group 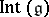 generated by them are called inner automorphisms. It is a normal subgroup of
generated by them are called inner automorphisms. It is a normal subgroup of  .
.
If  is a real or complex Lie group with semi-simple Lie algebra, then the inner automorphisms constitute precisely the identity component of the group
is a real or complex Lie group with semi-simple Lie algebra, then the inner automorphisms constitute precisely the identity component of the group 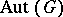 of automorphisms of
of automorphisms of 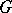 .
.
References
| [a1] | M. Hall jr., "The theory of groups" , Macmillan (1959) |
| [a2] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) pp. §5.4 |
| [a3] | J.-P. Serre, "Algèbres de Lie semi-simples complexes" , Benjamin (1966) |
Inner automorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inner_automorphism&oldid=15849