Infinite game
A non-cooperative game, in particular a two-person zero-sum game, with infinite sets of player strategies. Let
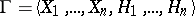 |
be an infinite game with  participants. It was shown by C. Berge [1] that if
participants. It was shown by C. Berge [1] that if  are locally convex compact linear topological Hausdorff spaces, if the pay-off functions
are locally convex compact linear topological Hausdorff spaces, if the pay-off functions  are continuous on
are continuous on  and are quasi-concave for
and are quasi-concave for  ,
,  , then the game
, then the game  has equilibrium points (solutions). It was also shown [2] that if the
has equilibrium points (solutions). It was also shown [2] that if the  are compact Hausdorff spaces and the
are compact Hausdorff spaces and the 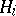 are continuous on
are continuous on 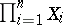 ,
,  , then
, then 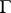 has equilibrium points in mixed strategies. However, not all infinite games have equilibrium points, even in mixed strategies. For example, for the two-person zero-sum game in which the sets of player strategies are sets of integers, while the pay-off function has the form
has equilibrium points in mixed strategies. However, not all infinite games have equilibrium points, even in mixed strategies. For example, for the two-person zero-sum game in which the sets of player strategies are sets of integers, while the pay-off function has the form
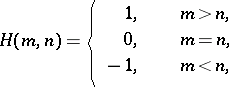 |
no value exists. The best studied classes of infinite games in normal form are infinite two-person zero-sum games and, in particular, games on the unit square (cf. Game on the unit square).
References
| [1] | C. Berge, "Théorie génerale des jeux à  personnes" , Gauthier-Villars (1957) personnes" , Gauthier-Villars (1957) |
| [2] | I.L. Gliksberg, "A further generalization of the Kakutani fixed point theorem with application to Nash equilibrium points" Proc. Amer. Math. Soc. , 3 : 1 (1952) pp. 170–174 |
Infinite game. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Infinite_game&oldid=13652