Infinite-dimensional space
A normal  -space
-space 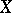 (cf. Normal space) such that for no
(cf. Normal space) such that for no 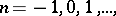 the inequality
the inequality 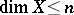 is satisfied, i.e.
is satisfied, i.e. 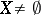 and for any
and for any 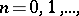 it is possible to find a finite open covering
it is possible to find a finite open covering 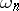 of
of 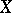 such that every finite covering refining
such that every finite covering refining 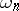 has multiplicity
has multiplicity 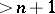 . Examples of infinite-dimensional spaces are the Hilbert cube
. Examples of infinite-dimensional spaces are the Hilbert cube 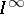 and the Tikhonov cube
and the Tikhonov cube 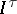 . Most of the spaces encountered in functional analysis are also infinite-dimensional.
. Most of the spaces encountered in functional analysis are also infinite-dimensional.
A normal 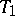 -space
-space 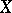 is said to be infinite-dimensional in the sense of the large (small) inductive dimension if the inequality
is said to be infinite-dimensional in the sense of the large (small) inductive dimension if the inequality 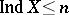 (
( ) is invalid for every
) is invalid for every 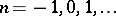 . If
. If 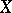 is an infinite-dimensional space, it is infinite-dimensional in the sense of the large inductive dimension. If in addition
is an infinite-dimensional space, it is infinite-dimensional in the sense of the large inductive dimension. If in addition 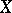 is compact, it is also infinite-dimensional in the sense of the small inductive dimension. The infinite dimensionality of a metric space is equivalent with its infinite dimensionality in the sense of the large inductive dimension. There exist finite-dimensional compacta that are infinite-dimensional in the sense of the small (and hence also in the sense of the large) inductive dimension. It is not known (1986) whether or not a compactum (or a metric space) that is finite-dimensional in the sense of the small inductive dimension and infinite-dimensional in the sense of the large inductive dimension exists.
is compact, it is also infinite-dimensional in the sense of the small inductive dimension. The infinite dimensionality of a metric space is equivalent with its infinite dimensionality in the sense of the large inductive dimension. There exist finite-dimensional compacta that are infinite-dimensional in the sense of the small (and hence also in the sense of the large) inductive dimension. It is not known (1986) whether or not a compactum (or a metric space) that is finite-dimensional in the sense of the small inductive dimension and infinite-dimensional in the sense of the large inductive dimension exists.
One of the most natural approaches to the study of infinite-dimensional spaces is to introduce the small transfinite dimension 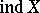 and the large transfinite dimension
and the large transfinite dimension 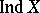 . This approach consists in the extension of the definition of small and large inductive dimensions to infinite ordinal numbers. The transfinite dimensions
. This approach consists in the extension of the definition of small and large inductive dimensions to infinite ordinal numbers. The transfinite dimensions 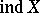 and
and  are not defined for all infinite-dimensional spaces. Thus, neither is defined for the Hilbert cube. The large transfinite dimension is not defined for the space
are not defined for all infinite-dimensional spaces. Thus, neither is defined for the Hilbert cube. The large transfinite dimension is not defined for the space 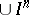 , which is the discrete sum of the
, which is the discrete sum of the  -dimensional cubes
-dimensional cubes 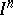 ,
, 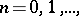 but
but 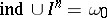 .
.
If the transfinite dimension 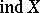 (
(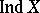 ) is defined for a normal space
) is defined for a normal space 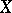 , then it is equal to an ordinal number whose cardinality does not exceed the weight
, then it is equal to an ordinal number whose cardinality does not exceed the weight 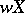 (respectively, the large weight
(respectively, the large weight 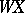 ) of
) of 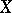 . In particular, if
. In particular, if 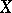 has a countable base, then
has a countable base, then 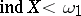 , and if
, and if 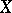 is compact, then
is compact, then 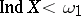 as well. For metric spaces, too,
as well. For metric spaces, too, 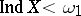 . If
. If 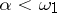 , then there exist compacta
, then there exist compacta 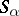 and
and 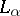 for which
for which 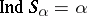 ,
, 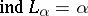 . For any ordinal number
. For any ordinal number 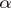 there exists a metric space
there exists a metric space 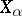 with
with  .
.
If the transfinite dimension 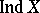 is defined, the transfinite dimension
is defined, the transfinite dimension 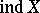 is defined as well, and
is defined as well, and 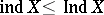 . Metric compacta for which the transfinite dimension
. Metric compacta for which the transfinite dimension 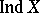 is defined and for which
is defined and for which 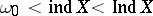 , have also been constructed.
, have also been constructed.
If the transfinite dimension 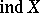 (
(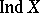 ) of a space
) of a space 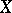 is defined, then also the transfinite dimension
is defined, then also the transfinite dimension 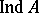 (
(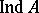 ) is defined for any (respectively, any closed) set
) is defined for any (respectively, any closed) set 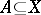 , and the inequality
, and the inequality 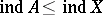 (or
(or 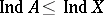 ) is valid.
) is valid.
For the maximal compactification 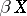 of a normal space
of a normal space 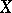 the equality
the equality 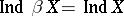 is valid. A normal space of weight
is valid. A normal space of weight  and of transfinite dimension
and of transfinite dimension 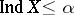 has a compactification
has a compactification 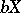 of weight
of weight  and dimension
and dimension 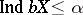 . There exists a space
. There exists a space  with a countable base having dimension
with a countable base having dimension 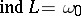 for which no compactification
for which no compactification 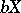 with a countable base has dimension
with a countable base has dimension 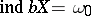 . A metrizable space
. A metrizable space 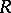 of transfinite dimension
of transfinite dimension 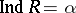 has a metric such that the completion
has a metric such that the completion 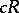 with respect to it has dimension
with respect to it has dimension 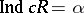 . A metrizable space
. A metrizable space 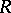 of transfinite dimension
of transfinite dimension 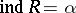 with a countable base has a metric such that the completion
with a countable base has a metric such that the completion 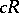 with respect to it has dimension
with respect to it has dimension 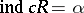 .
.
The class of spaces for which a large or a small transfinite dimension is defined is closely connected with the class of metric countable-dimensional spaces; if a complete metric space is countable-dimensional, then the small transfinite dimension is defined for it; if the small transfinite dimension is defined for a metric space with a countable base, the space is countable-dimensional; if for a metric space the large transfinite dimension is defined (in particular if the space is finite-dimensional), then the space is countable-dimensional; the large transfinite dimension is defined for a countable-dimensional metric compactum. The space 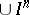 is countable-dimensional and is infinite-dimensional. The Hilbert cube is not countable-dimensional.
is countable-dimensional and is infinite-dimensional. The Hilbert cube is not countable-dimensional.
Countable dimensionality of a metric space 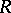 is equivalent to any one of the following properties: a) there exists a finite-to-one (but, in general, not a
is equivalent to any one of the following properties: a) there exists a finite-to-one (but, in general, not a 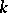 -to-one for any
-to-one for any 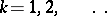 ) continuous closed mapping of a zero-dimensional metric space onto
) continuous closed mapping of a zero-dimensional metric space onto 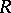 ; b) there exists a countable-to-one continuous closed mapping of a zero-dimensional metric space onto
; b) there exists a countable-to-one continuous closed mapping of a zero-dimensional metric space onto 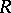 ; and c)
; and c) 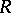 is a countably zero-dimensional space.
is a countably zero-dimensional space.
Theorems about the representability of any  -dimensional metric space as a sum of
-dimensional metric space as a sum of 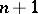 zero-dimensional subsets or as the image of a zero-dimensional metric space under a continuous closed
zero-dimensional subsets or as the image of a zero-dimensional metric space under a continuous closed 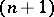 -to-one mapping indicate that it is natural to consider the class of countable-dimensional (metric) spaces and that it is close to the class of finite-dimensional spaces. As in the finite-dimensional case, there exists a countable-dimensional space which is universal in the sense of homeomorphic imbedding in the class of countable-dimensional metric spaces of weight
-to-one mapping indicate that it is natural to consider the class of countable-dimensional (metric) spaces and that it is close to the class of finite-dimensional spaces. As in the finite-dimensional case, there exists a countable-dimensional space which is universal in the sense of homeomorphic imbedding in the class of countable-dimensional metric spaces of weight 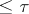 .
.
If a normal space is represented as a finite or a countable sum of its countable-dimensional subspaces, then it is countable-dimensional. A subspace of a countable-dimensional perfectly-normal space is countable-dimensional.
The following theorem describes the relationships between countable and non-countable dimensional metric spaces: If a mapping 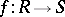 between metric spaces
between metric spaces 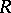 and
and 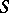 is continuous and closed, if the space
is continuous and closed, if the space  is countable-dimensional and the space
is countable-dimensional and the space  is non-countable dimensional, then the set
is non-countable dimensional, then the set  is also non-countable dimensional.
is also non-countable dimensional.
In addition to countable-dimensional spaces, a natural extension of the class of finite-dimensional spaces is the class of weakly countable-dimensional spaces. If one considers metrizable spaces only, weakly countable-dimensional spaces occupy a place which is intermediate between finite-dimensional and countable-dimensional spaces. There exist countable-dimensional metric compacta that are not weakly countable-dimensional, while the space 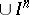 is both weakly countable-dimensional and infinite-dimensional. A closed subspace of a weakly countable-dimensional space is weakly countable-dimensional. A normal space is weakly countable-dimensional if it is representable as a finite or a countable sum of its weakly countable-dimensional closed subsets.
is both weakly countable-dimensional and infinite-dimensional. A closed subspace of a weakly countable-dimensional space is weakly countable-dimensional. A normal space is weakly countable-dimensional if it is representable as a finite or a countable sum of its weakly countable-dimensional closed subsets.
In the classes of normal weakly countable-dimensional and metric weakly countable-dimensional spaces there exist universal (in the sense of homeomorphic imbedding) spaces. In the case of spaces with a countable base, an example is the subspace 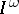 of the Hilbert cube which consists of all points with only a finite number of non-zero coordinates. The space
of the Hilbert cube which consists of all points with only a finite number of non-zero coordinates. The space 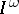 has no weakly countable-dimensional compactifications.
has no weakly countable-dimensional compactifications.
All classes of infinite-dimensional spaces considered so far are "not very infinite-dimensional" as compared with, for example, the Hilbert cube. The problem of distinguishing "not very infinite-dimensional" from "very infinite-dimensional" spaces was solved by P.S. Aleksandrov and Yu.M. Smirnov, who introduced the classes of 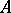 - and
- and 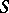 -weakly infinite-dimensional and of
-weakly infinite-dimensional and of 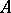 - and
- and 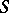 -strongly infinite-dimensional normal spaces. Any finite-dimensional space is
-strongly infinite-dimensional normal spaces. Any finite-dimensional space is 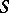 -weakly infinite-dimensional, while any
-weakly infinite-dimensional, while any 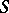 -weakly infinite-dimensional space is also
-weakly infinite-dimensional space is also 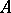 -weakly infinite-dimensional. The space
-weakly infinite-dimensional. The space  is
is 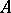 -weakly infinite-dimensional, but
-weakly infinite-dimensional, but 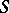 -strongly infinite-dimensional.
-strongly infinite-dimensional.
In the case of compacta the definitions of 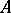 - and
- and 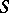 -weak (strong) infinite dimensionality are equivalent, and for this reason
-weak (strong) infinite dimensionality are equivalent, and for this reason 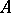 -weakly (strongly) infinite-dimensional compacta are simply called strongly (weakly) infinite-dimensional. The Hilbert cube is strongly infinite-dimensional. There exist infinite-dimensional and weakly infinite-dimensional compacta.
-weakly (strongly) infinite-dimensional compacta are simply called strongly (weakly) infinite-dimensional. The Hilbert cube is strongly infinite-dimensional. There exist infinite-dimensional and weakly infinite-dimensional compacta.
A closed subspace of an  - (
- (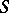 -) weakly infinite-dimensional space is
-) weakly infinite-dimensional space is 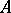 - (
- (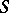 -) weakly infinite-dimensional. A normal space which is the sum of a finite number of its closed
-) weakly infinite-dimensional. A normal space which is the sum of a finite number of its closed 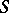 -weakly infinite-dimensional sets, is itself
-weakly infinite-dimensional sets, is itself  -weakly infinite-dimensional. A paracompactum which is the sum of a finite or countable system of its closed
-weakly infinite-dimensional. A paracompactum which is the sum of a finite or countable system of its closed  -weakly infinite-dimensional sets is itself
-weakly infinite-dimensional sets is itself 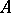 -weakly infinite-dimensional. A hereditarily-normal space which is the sum of a finite or countable system of its
-weakly infinite-dimensional. A hereditarily-normal space which is the sum of a finite or countable system of its 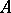 -weakly infinite-dimensional sets is itself
-weakly infinite-dimensional sets is itself 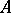 -weakly infinite-dimensional.
-weakly infinite-dimensional.
A weakly countable-dimensional paracompactum is 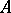 -weakly infinite-dimensional. A hereditarily-normal countable-dimensional space is
-weakly infinite-dimensional. A hereditarily-normal countable-dimensional space is 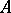 -weakly infinite-dimensional. A weakly infinite-dimensional, not countable-dimensional metric compactum has been constructed by R. Pol [3].
-weakly infinite-dimensional. A weakly infinite-dimensional, not countable-dimensional metric compactum has been constructed by R. Pol [3].
The study of arbitrary 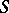 -weakly infinite-dimensional metrizable spaces is reduced to the compact case by the following: A metrizable space
-weakly infinite-dimensional metrizable spaces is reduced to the compact case by the following: A metrizable space  is
is 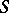 -weakly infinite-dimensional if and only if it can be represented as a sum of a weakly infinite-dimensional compactum and finite-dimensional open sets
-weakly infinite-dimensional if and only if it can be represented as a sum of a weakly infinite-dimensional compactum and finite-dimensional open sets 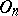 ,
,  such that for any discrete sequence of points
such that for any discrete sequence of points
 |
there exists a set 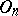 (depending on the sequence) containing all the points
(depending on the sequence) containing all the points 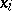 , beginning with some such point.
, beginning with some such point.
The following theorems provide another way of studying infinite-dimensional compacta instead of arbitrary 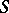 -weakly infinite-dimensional spaces: The maximal compactification of an
-weakly infinite-dimensional spaces: The maximal compactification of an 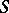 -weakly infinite-dimensional space is weakly infinite-dimensional; any normal
-weakly infinite-dimensional space is weakly infinite-dimensional; any normal 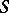 -weakly infinite-dimensional space of weight
-weakly infinite-dimensional space of weight  has a weakly infinite-dimensional compactification of weight
has a weakly infinite-dimensional compactification of weight  . All compactifications of the
. All compactifications of the  -weakly infinite-dimensional space
-weakly infinite-dimensional space 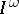 are strongly infinite-dimensional.
are strongly infinite-dimensional.
A compactum is strongly infinite-dimensional if and only if there exists a continuous mapping 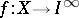 such that for any set
such that for any set
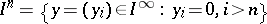 |
(which is homeomorphic to an  -dimensional cube) the restriction of the mapping
-dimensional cube) the restriction of the mapping 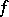 to the inverse image
to the inverse image 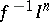 is an essential mapping.
is an essential mapping.
There exists an infinite-dimensional metric compactum any non-empty subspace of which is either zero-dimensional or infinite-dimensional. Moreover, any strongly infinite-dimensional metric compactum contains a subcompactum any non-empty subspace of which is either zero-dimensional or infinite-dimensional. Any strongly infinite-dimensional compactum contains an infinite-dimensional Cantor manifold.
All separable Banach spaces are mutually homeomorphic, 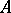 -strongly infinite-dimensional and homeomorphic to the product of a countable system of straight lines.
-strongly infinite-dimensional and homeomorphic to the product of a countable system of straight lines.
References
| [1] | P.S. Aleksandrov, B.A. Pasynkov, "Introduction to dimension theory" , Moscow (1973) (In Russian) |
| [2] | R. Engelking, "Transfinite dimension" G.M. Reed (ed.) , Surveys in general topology , Acad. Press (1980) pp. 131–161 |
| [3] | R. Pol, "A weakly infinite-dimensional compactum which is not countable dimensional" Proc. Amer. Math. Soc. , 82 (1981) pp. 634–636 |
Comments
A space is called a countable-dimensional space if it can be written as the union of a countable family of finite-dimensional subsets, see also Countably zero-dimensional space.
References
| [a1] | R. Engelking, "Dimension theory" , North-Holland & PWN (1978) |
| [a2] | R. Engelking, E. Pol, "Countable dimensional spaces: a survey" Diss. Math. , 216 (1983) pp. 1–41 |
| [a3] | L.A. Ljuksemburg, "On compact metric spaces with non-coinciding transfinite dimensions" Pac. J. Math. , 93 (1981) pp. 339–386 |
| [a4] | C. Bessaga, A. Pelczyński, "Selected topics in infinite-dimensional topology" , PWN (1975) |
Infinite-dimensional space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Infinite-dimensional_space&oldid=19081