|
|
| (3 intermediate revisions by 3 users not shown) |
| Line 1: |
Line 1: |
| − | A function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i0503101.png" /> given by an equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i0503102.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i0503103.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i0503104.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i0503105.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i0503106.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i0503107.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i0503108.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i0503109.png" /> are certain sets, i.e. a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031010.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031011.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031012.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031013.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031014.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031015.png" /> are topological spaces and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031016.png" /> for some point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031017.png" />, then under certain conditions the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031018.png" /> is uniquely solvable in one of the variables in some neighbourhood of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031019.png" />. Properties of the solution of this equation are described by implicit-function theorems.
| + | <!-- |
| | + | i0503101.png |
| | + | $#A+1 = 221 n = 0 |
| | + | $#C+1 = 221 : ~/encyclopedia/old_files/data/I050/I.0500310 Implicit function |
| | + | Automatically converted into TeX, above some diagnostics. |
| | + | Please remove this comment and the {{TEX|auto}} line below, |
| | + | if TeX found to be correct. |
| | + | --> |
| | | | |
| − | The simplest implicit-function theorem is as follows. Suppose that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031020.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031021.png" /> are subsets of the real line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031022.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031023.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031024.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031025.png" /> be an interior point of the plane set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031026.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031027.png" /> is continuous in some neighbourhood of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031028.png" />, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031029.png" /> and if there are a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031030.png" /> and an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031031.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031032.png" />, for any fixed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031033.png" />, is strictly monotone on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031034.png" /> as a function of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031035.png" />, then there is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031036.png" /> such that there is a unique function
| + | {{TEX|auto}} |
| | + | {{TEX|done}} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031037.png" /></td> </tr></table>
| + | A function $ f : E \rightarrow Y $ |
| | + | given by an equation $ F ( x , y ) = z _ {0} $, |
| | + | where $ F: X \times Y \rightarrow Z $, |
| | + | $ x \in X $, |
| | + | $ y \in Y $, |
| | + | $ E \subset X $, |
| | + | and $ X $, |
| | + | $ Y $ |
| | + | and $ Z $ |
| | + | are certain sets, i.e. a function $ f $ |
| | + | such that $ F ( x , f ( x) ) = z _ {0} $ |
| | + | for any $ x \in E $. |
| | + | If $ X $, |
| | + | $ Y $ |
| | + | and $ Z $ |
| | + | are topological spaces and if $ F ( x _ {0} , y _ {0} ) = z _ {0} $ |
| | + | for some point $ ( x _ {0} , y _ {0} ) \in X \times Y $, |
| | + | then under certain conditions the equation $ F ( x , y ) = z _ {0} $ |
| | + | is uniquely solvable in one of the variables in some neighbourhood of $ ( x _ {0} , y _ {0} ) $. |
| | + | Properties of the solution of this equation are described by implicit-function theorems. |
| | | | |
| − | for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031038.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031039.png" />; moreover, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031040.png" /> is continuous and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031041.png" />. | + | The simplest implicit-function theorem is as follows. Suppose that $ X $ |
| | + | and $ Y $ |
| | + | are subsets of the real line $ \mathbf R $, |
| | + | let $ x _ {0} \in X $, |
| | + | $ y _ {0} \in Y $, |
| | + | and let $ ( x _ {0} , y _ {0} ) $ |
| | + | be an interior point of the plane set $ X \times Y $; |
| | + | if $ F $ |
| | + | is continuous in some neighbourhood of $ ( x _ {0} , y _ {0} ) $, |
| | + | if $ F ( x _ {0} , y _ {0} ) = 0 $ |
| | + | and if there are a $ \delta > 0 $ |
| | + | and an $ \epsilon > 0 $ |
| | + | such that $ F ( x , y ) $, |
| | + | for any fixed $ x \in ( x _ {0} - \delta , x _ {0} + \delta ) $, |
| | + | is strictly monotone on $ ( y _ {0} - \epsilon , y _ {0} + \epsilon ) $ |
| | + | as a function of $ y $, |
| | + | then there is a $ \delta _ {0} > 0 $ |
| | + | such that there is a unique function |
| | + | |
| | + | $$ |
| | + | f : ( x _ {0} - \delta _ {0} , x _ {0} + \delta _ {0} ) \rightarrow \ |
| | + | ( y _ {0} - \epsilon , y _ {0} + \epsilon ) |
| | + | $$ |
| | + | |
| | + | for which $ F ( x , f ( x) ) = 0 $ |
| | + | for all $ x \in ( x _ {0} - \delta _ {0} , x _ {0} + \delta _ {0} ) $; |
| | + | moreover, $ f $ |
| | + | is continuous and $ f ( x _ {0} ) = y _ {0} $. |
| | | | |
| | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/i050310a.gif" /> | | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/i050310a.gif" /> |
| Line 11: |
Line 65: |
| | Figure: i050310a | | Figure: i050310a |
| | | | |
| − | The hypotheses of this theorem are satisfied if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031042.png" /> is continuous in a neighbourhood of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031043.png" />, if the partial derivative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031044.png" /> exists and is continuous at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031045.png" />, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031046.png" />, and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031047.png" />. If in addition the partial derivative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031048.png" /> exists and is continuous at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031049.png" />, then the implicit function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031050.png" /> is differentiable at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031051.png" />, and | + | The hypotheses of this theorem are satisfied if $ F $ |
| | + | is continuous in a neighbourhood of $ ( x _ {0} , y _ {0} ) $, |
| | + | if the partial derivative $ F _ {y} $ |
| | + | exists and is continuous at $ ( x _ {0} , y _ {0} ) $, |
| | + | if $ F ( x _ {0} , y _ {0} ) = 0 $, |
| | + | and if $ F _ {y} ( x _ {0} , y _ {0} ) \neq 0 $. |
| | + | If in addition the partial derivative $ F _ {x} $ |
| | + | exists and is continuous at $ ( x _ {0} , y _ {0} ) $, |
| | + | then the implicit function $ f $ |
| | + | is differentiable at $ x _ {0} $, |
| | + | and |
| | + | |
| | + | $$ |
| | + | |
| | + | \frac{d f ( x _ {0} ) }{dx} |
| | + | = - |
| | + | |
| | + | \frac{F _ {x} ( x _ {0} , y _ {0} ) }{F _ {y} ( x _ {0} , y _ {0} ) } |
| | + | . |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031052.png" /></td> </tr></table>
| + | This theorem has been generalized to the case of a system of equations, that is, when $ F $ |
| | + | is a vector function. Let $ \mathbf R ^ {n} $ |
| | + | and $ \mathbf R ^ {m} $ |
| | + | be $ n $- |
| | + | and $ m $- |
| | + | dimensional Euclidean spaces with fixed coordinate systems and points $ x = ( x _ {1} \dots x _ {n} ) $ |
| | + | and $ y = ( y _ {1} \dots y _ {m} ) $, |
| | + | respectively. Suppose that $ F $ |
| | + | maps a certain neighbourhood $ W $ |
| | + | of $ ( x _ {0} , y _ {0} ) \in \mathbf R ^ {n} \times \mathbf R ^ {m} $( |
| | + | $ x _ {0} \in \mathbf R ^ {n} $, |
| | + | $ y _ {0} \in \mathbf R ^ {m} $) |
| | + | into $ \mathbf R ^ {m} $ |
| | + | and that $ F _ {i} $, |
| | + | $ i = 1 \dots m $, |
| | + | are the coordinate functions (of the $ n + m $ |
| | + | variables $ x _ {1} \dots x _ {n} , y _ {1} \dots y _ {m} $) |
| | + | of $ F $, |
| | + | that is, $ F = ( F _ {1} \dots F _ {m} ) $. |
| | + | If $ F $ |
| | + | is differentiable on $ W $, |
| | + | if $ F( x _ {0} , y _ {0} ) = 0 $ |
| | + | and if the Jacobian |
| | | | |
| − | This theorem has been generalized to the case of a system of equations, that is, when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031053.png" /> is a vector function. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031054.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031055.png" /> be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031056.png" />- and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031057.png" />-dimensional Euclidean spaces with fixed coordinate systems and points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031058.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031059.png" />, respectively. Suppose that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031060.png" /> maps a certain neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031061.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031062.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031063.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031064.png" />) into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031065.png" /> and that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031066.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031067.png" />, are the coordinate functions (of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031068.png" /> variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031069.png" />) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031070.png" />, that is, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031071.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031072.png" /> is differentiable on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031073.png" />, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031074.png" /> and if the Jacobian
| + | $$ |
| | + | \left . |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031075.png" /></td> </tr></table>
| + | \frac{\partial ( F _ {1} \dots F _ {m} ) }{\partial ( y _ {1} \dots y _ {m} ) } |
| | | | |
| − | then there are neighbourhoods <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031076.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031077.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031078.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031079.png" />, respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031080.png" />, and a unique mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031081.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031082.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031083.png" />. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031084.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031085.png" /> is differentiable on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031086.png" />, and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031087.png" />, then the explicit expression for the partial derivatives <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031088.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031089.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031090.png" />, can be found from the system of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031091.png" /> linear equations in these derivatives:
| + | \right | _ {( x _ {0} , y _ {0} ) } \ |
| | + | \neq 0 , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031092.png" /></td> </tr></table>
| + | then there are neighbourhoods $ U $ |
| | + | and $ V $ |
| | + | of $ x _ {0} \in \mathbf R ^ {n} $ |
| | + | and $ y _ {0} \in \mathbf R ^ {m} $, |
| | + | respectively, $ U \times V \subset W $, |
| | + | and a unique mapping $ f : U \rightarrow V $ |
| | + | such that $ F ( x , f ( x) ) = 0 \in \mathbf R ^ {m} $ |
| | + | for all $ x \in U $. |
| | + | Here $ f ( x _ {0} ) = y _ {0} $, |
| | + | $ f $ |
| | + | is differentiable on $ U $, |
| | + | and if $ f = ( f _ {1} \dots f _ {m} ) $, |
| | + | then the explicit expression for the partial derivatives $ \partial f _ {j} / \partial x _ {i} $, |
| | + | $ i = 1 \dots n $, |
| | + | $ j = 1 \dots m $, |
| | + | can be found from the system of $ m $ |
| | + | linear equations in these derivatives: |
| | | | |
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031093.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031094.png" /> is fixed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031095.png" />. Sometimes the main assertion of the theorem is stated as follows: There are neighbourhoods <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031096.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031097.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031098.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i05031099.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310100.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310101.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310102.png" />, and a unique mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310103.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310104.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310105.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310106.png" />. In other words, the conditions
| + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310107.png" /></td> </tr></table>
| + | \frac{\partial F _ {k} }{\partial x _ {i} } |
| | + | + |
| | + | \sum_{j=}^ { m } |
| | | | |
| − | are equivalent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310108.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310109.png" />. In this case one says that the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310110.png" /> is uniquely solvable in the neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310111.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310112.png" />.
| + | \frac{\partial F _ {k} }{\partial y _ {j} } |
| | | | |
| − | The classical implicit-function theorem thus stated generalizes to the case of more general spaces in the following manner. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310113.png" /> be a topological space, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310114.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310115.png" /> be affine normed spaces over the field of real or complex numbers, that is, affine spaces over the relevant field to which are associated normed vector spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310116.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310117.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310118.png" /> being complete, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310119.png" /> be the set of continuous linear mappings from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310120.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310121.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310122.png" /> be an open set in the product space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310123.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310124.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310125.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310126.png" />.
| + | \frac{\partial f _ {j} }{\partial x _ {i} } |
| | + | = 0 , |
| | + | $$ |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310127.png" /> be a continuous mapping and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310128.png" />. If for every fixed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310129.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310130.png" /> the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310131.png" /> has a partial [[Fréchet derivative|Fréchet derivative]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310132.png" />, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310133.png" /> is a continuous mapping and if the linear mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310134.png" /> has a continuous inverse linear mapping (that is, it is an invertible element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310135.png" />), then there exist open sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310136.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310137.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310138.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310139.png" />, such that for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310140.png" /> there is a unique element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310141.png" />, denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310142.png" />, satisfying the equations
| + | $ k = 1 \dots m $, |
| | + | $ i $ |
| | + | is fixed $ ( i = 1 \dots n ) $. |
| | + | Sometimes the main assertion of the theorem is stated as follows: There are neighbourhoods $ U $ |
| | + | of $ x _ {0} $ |
| | + | in $ \mathbf R ^ {n} $ |
| | + | and $ W _ {0} $ |
| | + | of $ ( x _ {0} , y _ {0} ) $ |
| | + | in $ \mathbf R ^ {n} \times \mathbf R ^ {m} $, |
| | + | $ W _ {0} \subset W $, |
| | + | and a unique mapping $ f : U \rightarrow \mathbf R ^ {m} $ |
| | + | such that $ ( x , f ( x) ) \in W _ {0} $ |
| | + | and $ F ( x , f ( x) ) = 0 $ |
| | + | for all $ x \in U $. |
| | + | In other words, the conditions |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310143.png" /></td> </tr></table>
| + | $$ |
| | + | ( x , y ) \in W _ {0} ,\ \ |
| | + | F ( x , y ) = 0 |
| | + | $$ |
| | | | |
| − | The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310144.png" /> thus defined is a continuous mapping from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310145.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310146.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310147.png" />.
| + | are equivalent to $ x \in U $, |
| | + | $ y = f ( x) $. |
| | + | In this case one says that the equation $ F ( x , y ) = 0 $ |
| | + | is uniquely solvable in the neighbourhood $ W _ {0} $ |
| | + | of $ ( x _ {0} , y _ {0} ) $. |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310148.png" /> is also an affine normed space, then under certain conditions the implicit function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310149.png" /> which satisfies the equation
| + | The classical implicit-function theorem thus stated generalizes to the case of more general spaces in the following manner. Let $ X $ |
| | + | be a topological space, let $ Y $ |
| | + | and $ Z $ |
| | + | be affine normed spaces over the field of real or complex numbers, that is, affine spaces over the relevant field to which are associated normed vector spaces $ \mathbf Y $ |
| | + | and $ \mathbf Z $, |
| | + | $ \mathbf Y $ |
| | + | being complete, let $ {\mathcal L} ( \mathbf Y , \mathbf Z ) $ |
| | + | be the set of continuous linear mappings from $ \mathbf Y $ |
| | + | into $ \mathbf Z $, |
| | + | and let $ W $ |
| | + | be an open set in the product space $ X \times Y $, |
| | + | $ ( x _ {0} , y _ {0} ) \in W $, |
| | + | $ x _ {0} \in X $, |
| | + | $ y _ {0} \in Y $. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310150.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table>
| + | Let $ F : W \rightarrow Z $ |
| | + | be a continuous mapping and $ F ( x _ {0} , y _ {0} ) = z _ {0} $. |
| | + | If for every fixed $ x $ |
| | + | and $ ( x , y ) \in W $ |
| | + | the mapping $ F $ |
| | + | has a partial [[Fréchet derivative|Fréchet derivative]] $ F _ {y} \in {\mathcal L} ( \mathbf Y , \mathbf Z ) $, |
| | + | if $ F _ {y} ( x , y ) : W \rightarrow {\mathcal L} ( \mathbf Y , \mathbf Z ) $ |
| | + | is a continuous mapping and if the linear mapping $ F _ {y} ( x _ {0} , y _ {0} ) : \mathbf Y \rightarrow \mathbf Z $ |
| | + | has a continuous inverse linear mapping (that is, it is an invertible element of $ {\mathcal L} ( \mathbf Y , \mathbf Z ) $), |
| | + | then there exist open sets $ U \subset X $ |
| | + | and $ V \subset Y $, |
| | + | $ x _ {0} \in U $, |
| | + | $ y _ {0} \in V $, |
| | + | such that for any $ x \in U $ |
| | + | there is a unique element $ y \in V $, |
| | + | denoted by $ y = f ( x) $, |
| | + | satisfying the equations |
| | | | |
| − | is also differentiable. Namely, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310151.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310152.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310153.png" /> be affine normed spaces, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310154.png" /> be an open set in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310155.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310156.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310157.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310158.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310159.png" /> be the implicit mapping given by (1), taking a certain neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310160.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310161.png" /> into an open subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310162.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310163.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310164.png" />. Thus, for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310165.png" />,
| + | $$ |
| | + | f ( x) \in V \ \ |
| | + | \textrm{ and } \ F ( x , f ( x) ) = z _ {0} . |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310166.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table>
| + | The function $ y = f ( x) $ |
| | + | thus defined is a continuous mapping from $ U $ |
| | + | into $ V $, |
| | + | and $ y _ {0} = f ( x _ {0} ) $. |
| | | | |
| − | Suppose also that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310167.png" /> is continuous at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310168.png" /> and that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310169.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310170.png" /> is differentiable at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310171.png" />, if its partial Fréchet derivatives <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310172.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310173.png" /> are continuous linear operators taking the vector spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310174.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310175.png" /> associated with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310176.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310177.png" /> into the vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310178.png" /> associated with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310179.png" />, and if the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310180.png" /> is an invertible element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310181.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310182.png" /> is differentiable at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310183.png" /> and its Fréchet derivative is given by
| + | If $ X $ |
| | + | is also an affine normed space, then under certain conditions the implicit function $ f : x \mapsto y $ |
| | + | which satisfies the equation |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310184.png" /></td> </tr></table>
| + | $$ \tag{1 } |
| | + | F ( x , y ) = z _ {0} $$ |
| | | | |
| − | This is obtained as a result of formally differentiating (2):
| + | is also differentiable. Namely, let $ X $, |
| | + | $ Y $ |
| | + | and $ Z $ |
| | + | be affine normed spaces, let $ W $ |
| | + | be an open set in $ X \times Y $, |
| | + | let $ F : W \rightarrow Z $, |
| | + | $ F ( x _ {0} , y _ {0} ) = z _ {0} $, |
| | + | $ x _ {0} \in Y $, |
| | + | and let $ f $ |
| | + | be the implicit mapping given by (1), taking a certain neighbourhood $ U $ |
| | + | of $ x _ {0} $ |
| | + | into an open subset $ V $ |
| | + | of $ Y $, |
| | + | $ U \times V \subset W $. |
| | + | Thus, for all $ x \in U $, |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310185.png" /></td> </tr></table>
| + | $$ \tag{2 } |
| | + | f ( x) \in V ,\ \ |
| | + | F ( x , f ( x) ) = z _ {0} . |
| | + | $$ |
| | | | |
| − | and multiplying this equality on the left by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310186.png" />. | + | Suppose also that $ f $ |
| | + | is continuous at $ x _ {0} $ |
| | + | and that $ f ( x _ {0} ) = y _ {0} $. |
| | + | If $ F $ |
| | + | is differentiable at $ ( x _ {0} , y _ {0} ) $, |
| | + | if its partial Fréchet derivatives $ F _ {x} ( x _ {0} , y _ {0} ) $ |
| | + | and $ F _ {y} ( x _ {0} , y _ {0} ) $ |
| | + | are continuous linear operators taking the vector spaces $ \mathbf X $ |
| | + | and $ \mathbf Y $ |
| | + | associated with $ X $ |
| | + | and $ Y $ |
| | + | into the vector space $ \mathbf Z $ |
| | + | associated with $ Z $, |
| | + | and if the operator $ F _ {y} ( x _ {0} , y _ {0} ) $ |
| | + | is an invertible element of $ {\mathcal L} ( \mathbf Y , \mathbf Z ) $, |
| | + | then $ f $ |
| | + | is differentiable at $ x _ {0} $ |
| | + | and its Fréchet derivative is given by |
| | | | |
| − | If in addition the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310187.png" /> is continuously differentiable on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310188.png" />, if the implicit function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310189.png" /> is continuous on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310190.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310191.png" />, and if for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310192.png" /> the partial Fréchet derivative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310193.png" /> is an invertible element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310194.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310195.png" /> is a continuously-differentiable mapping of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310196.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310197.png" />.
| + | $$ |
| | + | f ^ { \prime } ( x _ {0} ) = \ |
| | + | - F _ {y} ^ { - 1 } |
| | + | ( x _ {0} , y _ {0} ) |
| | + | \circ F _ {x} ( x _ {0} , y _ {0} ) . |
| | + | $$ |
| | | | |
| − | In the general case one can also indicate conditions for the existence and the uniqueness of the implicit function in terms of the continuity of the Fréchet derivative: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310198.png" /> is complete, if the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310199.png" /> is continuously differentiable on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310200.png" />, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310201.png" />, and if the partial Fréchet derivative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310202.png" /> is an invertible element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310203.png" />, then (1) is uniquely solvable in a sufficiently small neighbourhood of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310204.png" />, i.e. there exist neighbourhoods <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310205.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310206.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310207.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310208.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310209.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310210.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310211.png" />, and a unique implicit function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310212.png" /> satisfying (2). Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310213.png" /> is also continuously differentiable on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310214.png" />. In this form the implicit-function theorem for normed spaces is a direct generalization of the corresponding classic implicit-function theorem for a single scalar equation in two variables.
| + | This is obtained as a result of formally differentiating (2): |
| | | | |
| − | Furthermore, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310215.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310216.png" />-times continuously-differentiable mapping in a neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310217.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310218.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310219.png" /> then the implicit function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310220.png" /> is also <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050310/i050310221.png" /> times continuously differentiable.
| + | $$ |
| | + | F _ {x} ( x _ {0} , y _ {0} ) + |
| | + | F _ {y} ( x _ {0} , y _ {0} ) |
| | + | \circ f ^ { \prime } ( x _ {0} ) = \ |
| | + | 0 \in {\mathcal L} ( \mathbf X , \mathbf Y ) |
| | + | $$ |
| | | | |
| − | Far-reaching generalizations of the classic implicit-function theorem to differential operators were given by J. Nash (see [[Nash theorems (in differential geometry)|Nash theorems (in differential geometry)]]).
| + | and multiplying this equality on the left by $ F _ {y} ^ { - 1 } ( x _ {0} , y _ {0} ) $. |
| | | | |
| − | ====References====
| + | If in addition the mapping $ F : W \rightarrow Z $ |
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , '''1–2''' , Graylock (1957–1961) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.A. Lyusternik, V.I. Sobolev, "Elemente der Funktionalanalysis" , Akademie Verlag (1968) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S.M. Nikol'skii, "A course of mathematical analysis" , '''1–2''' , MIR (1977) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> L. Schwartz, "Cours d'analyse" , '''1''' , Hermann (1967)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , '''1''' , MIR (1982) (Translated from Russian)</TD></TR></table>
| + | is continuously differentiable on $ W $, |
| | + | if the implicit function $ f : U \rightarrow V $ |
| | + | is continuous on $ U $, |
| | + | $ U \times X \subset W $, |
| | + | and if for any $ x \in U $ |
| | + | the partial Fréchet derivative $ F _ {y} ( x , f ( x) ) $ |
| | + | is an invertible element of $ {\mathcal L} ( \mathbf Y , \mathbf Z ) $, |
| | + | then $ f $ |
| | + | is a continuously-differentiable mapping of $ U $ |
| | + | into $ V $. |
| | | | |
| | + | In the general case one can also indicate conditions for the existence and the uniqueness of the implicit function in terms of the continuity of the Fréchet derivative: If $ Z $ |
| | + | is complete, if the mapping $ F : W \rightarrow Z $ |
| | + | is continuously differentiable on $ W $, |
| | + | if $ F ( x _ {0} , y _ {0} ) = z _ {0} $, |
| | + | and if the partial Fréchet derivative $ F _ {y} ( x _ {0} , y _ {0} ) $ |
| | + | is an invertible element of $ {\mathcal L} ( \mathbf Y , \mathbf Z ) $, |
| | + | then (1) is uniquely solvable in a sufficiently small neighbourhood of $ ( x _ {0} , y _ {0} ) $, |
| | + | i.e. there exist neighbourhoods $ U $ |
| | + | of $ x _ {0} $ |
| | + | in $ X $ |
| | + | and $ V $ |
| | + | of $ y _ {0} $ |
| | + | in $ Y $, |
| | + | $ U \times V \subset W $, |
| | + | and a unique implicit function $ f : U \rightarrow V $ |
| | + | satisfying (2). Here $ f $ |
| | + | is also continuously differentiable on $ U $. |
| | + | In this form the implicit-function theorem for normed spaces is a direct generalization of the corresponding classic implicit-function theorem for a single scalar equation in two variables. |
| | | | |
| | + | Furthermore, if $ F : W \rightarrow Z $ |
| | + | is a $ k $- |
| | + | times continuously-differentiable mapping in a neighbourhood $ W $ |
| | + | of $ ( x _ {0} , y _ {0} ) $, |
| | + | $ k = 1 , 2 \dots $ |
| | + | then the implicit function $ f : U \rightarrow V $ |
| | + | is also $ k $ |
| | + | times continuously differentiable. |
| | | | |
| − | ====Comments====
| + | Far-reaching generalizations of the classic implicit-function theorem to differential operators were given by J. Nash (see [[Nash theorems (in differential geometry)|Nash theorems (in differential geometry)]]). |
| | | | |
| | + | {{OldImage}} |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Fleming, "Functions of several variables" , Addison-Wesley (1965)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , '''1–2''' , Graylock (1957–1961) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.A. Lyusternik, V.I. Sobolev, "Elemente der Funktionalanalysis" , Akademie Verlag (1968) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S.M. Nikol'skii, "A course of mathematical analysis" , '''1–2''' , MIR (1977) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> L. Schwartz, "Cours d'analyse" , '''1''' , Hermann (1967)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , '''1''' , MIR (1982) (Translated from Russian)</TD></TR> |
| | + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Fleming, "Functions of several variables" , Addison-Wesley (1965)</TD><TR><TD valign="top">[a2]</TD> <TD valign="top"> T.M. Flett, "Differential Analysis" , Cambridge University Press (1980)</TD></TR></table> |
A function $ f : E \rightarrow Y $
given by an equation $ F ( x , y ) = z _ {0} $,
where $ F: X \times Y \rightarrow Z $,
$ x \in X $,
$ y \in Y $,
$ E \subset X $,
and $ X $,
$ Y $
and $ Z $
are certain sets, i.e. a function $ f $
such that $ F ( x , f ( x) ) = z _ {0} $
for any $ x \in E $.
If $ X $,
$ Y $
and $ Z $
are topological spaces and if $ F ( x _ {0} , y _ {0} ) = z _ {0} $
for some point $ ( x _ {0} , y _ {0} ) \in X \times Y $,
then under certain conditions the equation $ F ( x , y ) = z _ {0} $
is uniquely solvable in one of the variables in some neighbourhood of $ ( x _ {0} , y _ {0} ) $.
Properties of the solution of this equation are described by implicit-function theorems.
The simplest implicit-function theorem is as follows. Suppose that $ X $
and $ Y $
are subsets of the real line $ \mathbf R $,
let $ x _ {0} \in X $,
$ y _ {0} \in Y $,
and let $ ( x _ {0} , y _ {0} ) $
be an interior point of the plane set $ X \times Y $;
if $ F $
is continuous in some neighbourhood of $ ( x _ {0} , y _ {0} ) $,
if $ F ( x _ {0} , y _ {0} ) = 0 $
and if there are a $ \delta > 0 $
and an $ \epsilon > 0 $
such that $ F ( x , y ) $,
for any fixed $ x \in ( x _ {0} - \delta , x _ {0} + \delta ) $,
is strictly monotone on $ ( y _ {0} - \epsilon , y _ {0} + \epsilon ) $
as a function of $ y $,
then there is a $ \delta _ {0} > 0 $
such that there is a unique function
$$
f : ( x _ {0} - \delta _ {0} , x _ {0} + \delta _ {0} ) \rightarrow \
( y _ {0} - \epsilon , y _ {0} + \epsilon )
$$
for which $ F ( x , f ( x) ) = 0 $
for all $ x \in ( x _ {0} - \delta _ {0} , x _ {0} + \delta _ {0} ) $;
moreover, $ f $
is continuous and $ f ( x _ {0} ) = y _ {0} $.
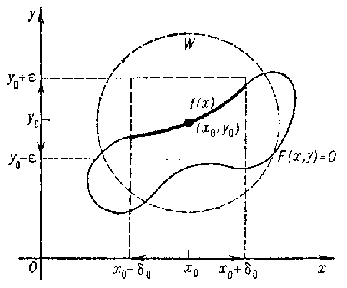
Figure: i050310a
The hypotheses of this theorem are satisfied if $ F $
is continuous in a neighbourhood of $ ( x _ {0} , y _ {0} ) $,
if the partial derivative $ F _ {y} $
exists and is continuous at $ ( x _ {0} , y _ {0} ) $,
if $ F ( x _ {0} , y _ {0} ) = 0 $,
and if $ F _ {y} ( x _ {0} , y _ {0} ) \neq 0 $.
If in addition the partial derivative $ F _ {x} $
exists and is continuous at $ ( x _ {0} , y _ {0} ) $,
then the implicit function $ f $
is differentiable at $ x _ {0} $,
and
$$
\frac{d f ( x _ {0} ) }{dx}
= -
\frac{F _ {x} ( x _ {0} , y _ {0} ) }{F _ {y} ( x _ {0} , y _ {0} ) }
.
$$
This theorem has been generalized to the case of a system of equations, that is, when $ F $
is a vector function. Let $ \mathbf R ^ {n} $
and $ \mathbf R ^ {m} $
be $ n $-
and $ m $-
dimensional Euclidean spaces with fixed coordinate systems and points $ x = ( x _ {1} \dots x _ {n} ) $
and $ y = ( y _ {1} \dots y _ {m} ) $,
respectively. Suppose that $ F $
maps a certain neighbourhood $ W $
of $ ( x _ {0} , y _ {0} ) \in \mathbf R ^ {n} \times \mathbf R ^ {m} $(
$ x _ {0} \in \mathbf R ^ {n} $,
$ y _ {0} \in \mathbf R ^ {m} $)
into $ \mathbf R ^ {m} $
and that $ F _ {i} $,
$ i = 1 \dots m $,
are the coordinate functions (of the $ n + m $
variables $ x _ {1} \dots x _ {n} , y _ {1} \dots y _ {m} $)
of $ F $,
that is, $ F = ( F _ {1} \dots F _ {m} ) $.
If $ F $
is differentiable on $ W $,
if $ F( x _ {0} , y _ {0} ) = 0 $
and if the Jacobian
$$
\left .
\frac{\partial ( F _ {1} \dots F _ {m} ) }{\partial ( y _ {1} \dots y _ {m} ) }
\right | _ {( x _ {0} , y _ {0} ) } \
\neq 0 ,
$$
then there are neighbourhoods $ U $
and $ V $
of $ x _ {0} \in \mathbf R ^ {n} $
and $ y _ {0} \in \mathbf R ^ {m} $,
respectively, $ U \times V \subset W $,
and a unique mapping $ f : U \rightarrow V $
such that $ F ( x , f ( x) ) = 0 \in \mathbf R ^ {m} $
for all $ x \in U $.
Here $ f ( x _ {0} ) = y _ {0} $,
$ f $
is differentiable on $ U $,
and if $ f = ( f _ {1} \dots f _ {m} ) $,
then the explicit expression for the partial derivatives $ \partial f _ {j} / \partial x _ {i} $,
$ i = 1 \dots n $,
$ j = 1 \dots m $,
can be found from the system of $ m $
linear equations in these derivatives:
$$
\frac{\partial F _ {k} }{\partial x _ {i} }
+
\sum_{j=}^ { m }
\frac{\partial F _ {k} }{\partial y _ {j} }
\frac{\partial f _ {j} }{\partial x _ {i} }
= 0 ,
$$
$ k = 1 \dots m $,
$ i $
is fixed $ ( i = 1 \dots n ) $.
Sometimes the main assertion of the theorem is stated as follows: There are neighbourhoods $ U $
of $ x _ {0} $
in $ \mathbf R ^ {n} $
and $ W _ {0} $
of $ ( x _ {0} , y _ {0} ) $
in $ \mathbf R ^ {n} \times \mathbf R ^ {m} $,
$ W _ {0} \subset W $,
and a unique mapping $ f : U \rightarrow \mathbf R ^ {m} $
such that $ ( x , f ( x) ) \in W _ {0} $
and $ F ( x , f ( x) ) = 0 $
for all $ x \in U $.
In other words, the conditions
$$
( x , y ) \in W _ {0} ,\ \
F ( x , y ) = 0
$$
are equivalent to $ x \in U $,
$ y = f ( x) $.
In this case one says that the equation $ F ( x , y ) = 0 $
is uniquely solvable in the neighbourhood $ W _ {0} $
of $ ( x _ {0} , y _ {0} ) $.
The classical implicit-function theorem thus stated generalizes to the case of more general spaces in the following manner. Let $ X $
be a topological space, let $ Y $
and $ Z $
be affine normed spaces over the field of real or complex numbers, that is, affine spaces over the relevant field to which are associated normed vector spaces $ \mathbf Y $
and $ \mathbf Z $,
$ \mathbf Y $
being complete, let $ {\mathcal L} ( \mathbf Y , \mathbf Z ) $
be the set of continuous linear mappings from $ \mathbf Y $
into $ \mathbf Z $,
and let $ W $
be an open set in the product space $ X \times Y $,
$ ( x _ {0} , y _ {0} ) \in W $,
$ x _ {0} \in X $,
$ y _ {0} \in Y $.
Let $ F : W \rightarrow Z $
be a continuous mapping and $ F ( x _ {0} , y _ {0} ) = z _ {0} $.
If for every fixed $ x $
and $ ( x , y ) \in W $
the mapping $ F $
has a partial Fréchet derivative $ F _ {y} \in {\mathcal L} ( \mathbf Y , \mathbf Z ) $,
if $ F _ {y} ( x , y ) : W \rightarrow {\mathcal L} ( \mathbf Y , \mathbf Z ) $
is a continuous mapping and if the linear mapping $ F _ {y} ( x _ {0} , y _ {0} ) : \mathbf Y \rightarrow \mathbf Z $
has a continuous inverse linear mapping (that is, it is an invertible element of $ {\mathcal L} ( \mathbf Y , \mathbf Z ) $),
then there exist open sets $ U \subset X $
and $ V \subset Y $,
$ x _ {0} \in U $,
$ y _ {0} \in V $,
such that for any $ x \in U $
there is a unique element $ y \in V $,
denoted by $ y = f ( x) $,
satisfying the equations
$$
f ( x) \in V \ \
\textrm{ and } \ F ( x , f ( x) ) = z _ {0} .
$$
The function $ y = f ( x) $
thus defined is a continuous mapping from $ U $
into $ V $,
and $ y _ {0} = f ( x _ {0} ) $.
If $ X $
is also an affine normed space, then under certain conditions the implicit function $ f : x \mapsto y $
which satisfies the equation
$$ \tag{1 }
F ( x , y ) = z _ {0} $$
is also differentiable. Namely, let $ X $,
$ Y $
and $ Z $
be affine normed spaces, let $ W $
be an open set in $ X \times Y $,
let $ F : W \rightarrow Z $,
$ F ( x _ {0} , y _ {0} ) = z _ {0} $,
$ x _ {0} \in Y $,
and let $ f $
be the implicit mapping given by (1), taking a certain neighbourhood $ U $
of $ x _ {0} $
into an open subset $ V $
of $ Y $,
$ U \times V \subset W $.
Thus, for all $ x \in U $,
$$ \tag{2 }
f ( x) \in V ,\ \
F ( x , f ( x) ) = z _ {0} .
$$
Suppose also that $ f $
is continuous at $ x _ {0} $
and that $ f ( x _ {0} ) = y _ {0} $.
If $ F $
is differentiable at $ ( x _ {0} , y _ {0} ) $,
if its partial Fréchet derivatives $ F _ {x} ( x _ {0} , y _ {0} ) $
and $ F _ {y} ( x _ {0} , y _ {0} ) $
are continuous linear operators taking the vector spaces $ \mathbf X $
and $ \mathbf Y $
associated with $ X $
and $ Y $
into the vector space $ \mathbf Z $
associated with $ Z $,
and if the operator $ F _ {y} ( x _ {0} , y _ {0} ) $
is an invertible element of $ {\mathcal L} ( \mathbf Y , \mathbf Z ) $,
then $ f $
is differentiable at $ x _ {0} $
and its Fréchet derivative is given by
$$
f ^ { \prime } ( x _ {0} ) = \
- F _ {y} ^ { - 1 }
( x _ {0} , y _ {0} )
\circ F _ {x} ( x _ {0} , y _ {0} ) .
$$
This is obtained as a result of formally differentiating (2):
$$
F _ {x} ( x _ {0} , y _ {0} ) +
F _ {y} ( x _ {0} , y _ {0} )
\circ f ^ { \prime } ( x _ {0} ) = \
0 \in {\mathcal L} ( \mathbf X , \mathbf Y )
$$
and multiplying this equality on the left by $ F _ {y} ^ { - 1 } ( x _ {0} , y _ {0} ) $.
If in addition the mapping $ F : W \rightarrow Z $
is continuously differentiable on $ W $,
if the implicit function $ f : U \rightarrow V $
is continuous on $ U $,
$ U \times X \subset W $,
and if for any $ x \in U $
the partial Fréchet derivative $ F _ {y} ( x , f ( x) ) $
is an invertible element of $ {\mathcal L} ( \mathbf Y , \mathbf Z ) $,
then $ f $
is a continuously-differentiable mapping of $ U $
into $ V $.
In the general case one can also indicate conditions for the existence and the uniqueness of the implicit function in terms of the continuity of the Fréchet derivative: If $ Z $
is complete, if the mapping $ F : W \rightarrow Z $
is continuously differentiable on $ W $,
if $ F ( x _ {0} , y _ {0} ) = z _ {0} $,
and if the partial Fréchet derivative $ F _ {y} ( x _ {0} , y _ {0} ) $
is an invertible element of $ {\mathcal L} ( \mathbf Y , \mathbf Z ) $,
then (1) is uniquely solvable in a sufficiently small neighbourhood of $ ( x _ {0} , y _ {0} ) $,
i.e. there exist neighbourhoods $ U $
of $ x _ {0} $
in $ X $
and $ V $
of $ y _ {0} $
in $ Y $,
$ U \times V \subset W $,
and a unique implicit function $ f : U \rightarrow V $
satisfying (2). Here $ f $
is also continuously differentiable on $ U $.
In this form the implicit-function theorem for normed spaces is a direct generalization of the corresponding classic implicit-function theorem for a single scalar equation in two variables.
Furthermore, if $ F : W \rightarrow Z $
is a $ k $-
times continuously-differentiable mapping in a neighbourhood $ W $
of $ ( x _ {0} , y _ {0} ) $,
$ k = 1 , 2 \dots $
then the implicit function $ f : U \rightarrow V $
is also $ k $
times continuously differentiable.
Far-reaching generalizations of the classic implicit-function theorem to differential operators were given by J. Nash (see Nash theorems (in differential geometry)).
🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️
References
| [1] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [2] | L.A. Lyusternik, V.I. Sobolev, "Elemente der Funktionalanalysis" , Akademie Verlag (1968) (Translated from Russian) |
| [3] | S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian) |
| [4] | L. Schwartz, "Cours d'analyse" , 1 , Hermann (1967) |
| [5] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1 , MIR (1982) (Translated from Russian) |
| [a1] | W. Fleming, "Functions of several variables" , Addison-Wesley (1965) |
| [a2] | T.M. Flett, "Differential Analysis" , Cambridge University Press (1980) |
