Implicit function
A function $ f : E \rightarrow Y $
given by an equation $ F ( x , y ) = z _ {0} $,
where $ F: X \times Y \rightarrow Z $,
$ x \in X $,
$ y \in Y $,
$ E \subset X $,
and $ X $,
$ Y $
and $ Z $
are certain sets, i.e. a function $ f $
such that $ F ( x , f ( x) ) = z _ {0} $
for any $ x \in E $.
If $ X $,
$ Y $
and $ Z $
are topological spaces and if $ F ( x _ {0} , y _ {0} ) = z _ {0} $
for some point $ ( x _ {0} , y _ {0} ) \in X \times Y $,
then under certain conditions the equation $ F ( x , y ) = z _ {0} $
is uniquely solvable in one of the variables in some neighbourhood of $ ( x _ {0} , y _ {0} ) $.
Properties of the solution of this equation are described by implicit-function theorems.
The simplest implicit-function theorem is as follows. Suppose that $ X $ and $ Y $ are subsets of the real line $ \mathbf R $, let $ x _ {0} \in X $, $ y _ {0} \in Y $, and let $ ( x _ {0} , y _ {0} ) $ be an interior point of the plane set $ X \times Y $; if $ F $ is continuous in some neighbourhood of $ ( x _ {0} , y _ {0} ) $, if $ F ( x _ {0} , y _ {0} ) = 0 $ and if there are a $ \delta > 0 $ and an $ \epsilon > 0 $ such that $ F ( x , y ) $, for any fixed $ x \in ( x _ {0} - \delta , x _ {0} + \delta ) $, is strictly monotone on $ ( y _ {0} - \epsilon , y _ {0} + \epsilon ) $ as a function of $ y $, then there is a $ \delta _ {0} > 0 $ such that there is a unique function
$$ f : ( x _ {0} - \delta _ {0} , x _ {0} + \delta _ {0} ) \rightarrow \ ( y _ {0} - \epsilon , y _ {0} + \epsilon ) $$
for which $ F ( x , f ( x) ) = 0 $ for all $ x \in ( x _ {0} - \delta _ {0} , x _ {0} + \delta _ {0} ) $; moreover, $ f $ is continuous and $ f ( x _ {0} ) = y _ {0} $.
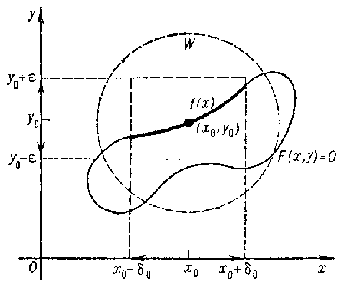
Figure: i050310a
The hypotheses of this theorem are satisfied if $ F $ is continuous in a neighbourhood of $ ( x _ {0} , y _ {0} ) $, if the partial derivative $ F _ {y} $ exists and is continuous at $ ( x _ {0} , y _ {0} ) $, if $ F ( x _ {0} , y _ {0} ) = 0 $, and if $ F _ {y} ( x _ {0} , y _ {0} ) \neq 0 $. If in addition the partial derivative $ F _ {x} $ exists and is continuous at $ ( x _ {0} , y _ {0} ) $, then the implicit function $ f $ is differentiable at $ x _ {0} $, and
$$ \frac{d f ( x _ {0} ) }{dx} = - \frac{F _ {x} ( x _ {0} , y _ {0} ) }{F _ {y} ( x _ {0} , y _ {0} ) } . $$
This theorem has been generalized to the case of a system of equations, that is, when $ F $ is a vector function. Let $ \mathbf R ^ {n} $ and $ \mathbf R ^ {m} $ be $ n $- and $ m $- dimensional Euclidean spaces with fixed coordinate systems and points $ x = ( x _ {1} \dots x _ {n} ) $ and $ y = ( y _ {1} \dots y _ {m} ) $, respectively. Suppose that $ F $ maps a certain neighbourhood $ W $ of $ ( x _ {0} , y _ {0} ) \in \mathbf R ^ {n} \times \mathbf R ^ {m} $( $ x _ {0} \in \mathbf R ^ {n} $, $ y _ {0} \in \mathbf R ^ {m} $) into $ \mathbf R ^ {m} $ and that $ F _ {i} $, $ i = 1 \dots m $, are the coordinate functions (of the $ n + m $ variables $ x _ {1} \dots x _ {n} , y _ {1} \dots y _ {m} $) of $ F $, that is, $ F = ( F _ {1} \dots F _ {m} ) $. If $ F $ is differentiable on $ W $, if $ F( x _ {0} , y _ {0} ) = 0 $ and if the Jacobian
$$ \left . \frac{\partial ( F _ {1} \dots F _ {m} ) }{\partial ( y _ {1} \dots y _ {m} ) } \right | _ {( x _ {0} , y _ {0} ) } \ \neq 0 , $$
then there are neighbourhoods $ U $ and $ V $ of $ x _ {0} \in \mathbf R ^ {n} $ and $ y _ {0} \in \mathbf R ^ {m} $, respectively, $ U \times V \subset W $, and a unique mapping $ f : U \rightarrow V $ such that $ F ( x , f ( x) ) = 0 \in \mathbf R ^ {m} $ for all $ x \in U $. Here $ f ( x _ {0} ) = y _ {0} $, $ f $ is differentiable on $ U $, and if $ f = ( f _ {1} \dots f _ {m} ) $, then the explicit expression for the partial derivatives $ \partial f _ {j} / \partial x _ {i} $, $ i = 1 \dots n $, $ j = 1 \dots m $, can be found from the system of $ m $ linear equations in these derivatives:
$$ \frac{\partial F _ {k} }{\partial x _ {i} } + \sum_{j=}^ { m } \frac{\partial F _ {k} }{\partial y _ {j} } \frac{\partial f _ {j} }{\partial x _ {i} } = 0 , $$
$ k = 1 \dots m $, $ i $ is fixed $ ( i = 1 \dots n ) $. Sometimes the main assertion of the theorem is stated as follows: There are neighbourhoods $ U $ of $ x _ {0} $ in $ \mathbf R ^ {n} $ and $ W _ {0} $ of $ ( x _ {0} , y _ {0} ) $ in $ \mathbf R ^ {n} \times \mathbf R ^ {m} $, $ W _ {0} \subset W $, and a unique mapping $ f : U \rightarrow \mathbf R ^ {m} $ such that $ ( x , f ( x) ) \in W _ {0} $ and $ F ( x , f ( x) ) = 0 $ for all $ x \in U $. In other words, the conditions
$$ ( x , y ) \in W _ {0} ,\ \ F ( x , y ) = 0 $$
are equivalent to $ x \in U $, $ y = f ( x) $. In this case one says that the equation $ F ( x , y ) = 0 $ is uniquely solvable in the neighbourhood $ W _ {0} $ of $ ( x _ {0} , y _ {0} ) $.
The classical implicit-function theorem thus stated generalizes to the case of more general spaces in the following manner. Let $ X $ be a topological space, let $ Y $ and $ Z $ be affine normed spaces over the field of real or complex numbers, that is, affine spaces over the relevant field to which are associated normed vector spaces $ \mathbf Y $ and $ \mathbf Z $, $ \mathbf Y $ being complete, let $ {\mathcal L} ( \mathbf Y , \mathbf Z ) $ be the set of continuous linear mappings from $ \mathbf Y $ into $ \mathbf Z $, and let $ W $ be an open set in the product space $ X \times Y $, $ ( x _ {0} , y _ {0} ) \in W $, $ x _ {0} \in X $, $ y _ {0} \in Y $.
Let $ F : W \rightarrow Z $ be a continuous mapping and $ F ( x _ {0} , y _ {0} ) = z _ {0} $. If for every fixed $ x $ and $ ( x , y ) \in W $ the mapping $ F $ has a partial Fréchet derivative $ F _ {y} \in {\mathcal L} ( \mathbf Y , \mathbf Z ) $, if $ F _ {y} ( x , y ) : W \rightarrow {\mathcal L} ( \mathbf Y , \mathbf Z ) $ is a continuous mapping and if the linear mapping $ F _ {y} ( x _ {0} , y _ {0} ) : \mathbf Y \rightarrow \mathbf Z $ has a continuous inverse linear mapping (that is, it is an invertible element of $ {\mathcal L} ( \mathbf Y , \mathbf Z ) $), then there exist open sets $ U \subset X $ and $ V \subset Y $, $ x _ {0} \in U $, $ y _ {0} \in V $, such that for any $ x \in U $ there is a unique element $ y \in V $, denoted by $ y = f ( x) $, satisfying the equations
$$ f ( x) \in V \ \ \textrm{ and } \ F ( x , f ( x) ) = z _ {0} . $$
The function $ y = f ( x) $ thus defined is a continuous mapping from $ U $ into $ V $, and $ y _ {0} = f ( x _ {0} ) $.
If $ X $ is also an affine normed space, then under certain conditions the implicit function $ f : x \mapsto y $ which satisfies the equation
$$ \tag{1 } F ( x , y ) = z _ {0} $$
is also differentiable. Namely, let $ X $, $ Y $ and $ Z $ be affine normed spaces, let $ W $ be an open set in $ X \times Y $, let $ F : W \rightarrow Z $, $ F ( x _ {0} , y _ {0} ) = z _ {0} $, $ x _ {0} \in Y $, and let $ f $ be the implicit mapping given by (1), taking a certain neighbourhood $ U $ of $ x _ {0} $ into an open subset $ V $ of $ Y $, $ U \times V \subset W $. Thus, for all $ x \in U $,
$$ \tag{2 } f ( x) \in V ,\ \ F ( x , f ( x) ) = z _ {0} . $$
Suppose also that $ f $ is continuous at $ x _ {0} $ and that $ f ( x _ {0} ) = y _ {0} $. If $ F $ is differentiable at $ ( x _ {0} , y _ {0} ) $, if its partial Fréchet derivatives $ F _ {x} ( x _ {0} , y _ {0} ) $ and $ F _ {y} ( x _ {0} , y _ {0} ) $ are continuous linear operators taking the vector spaces $ \mathbf X $ and $ \mathbf Y $ associated with $ X $ and $ Y $ into the vector space $ \mathbf Z $ associated with $ Z $, and if the operator $ F _ {y} ( x _ {0} , y _ {0} ) $ is an invertible element of $ {\mathcal L} ( \mathbf Y , \mathbf Z ) $, then $ f $ is differentiable at $ x _ {0} $ and its Fréchet derivative is given by
$$ f ^ { \prime } ( x _ {0} ) = \ - F _ {y} ^ { - 1 } ( x _ {0} , y _ {0} ) \circ F _ {x} ( x _ {0} , y _ {0} ) . $$
This is obtained as a result of formally differentiating (2):
$$ F _ {x} ( x _ {0} , y _ {0} ) + F _ {y} ( x _ {0} , y _ {0} ) \circ f ^ { \prime } ( x _ {0} ) = \ 0 \in {\mathcal L} ( \mathbf X , \mathbf Y ) $$
and multiplying this equality on the left by $ F _ {y} ^ { - 1 } ( x _ {0} , y _ {0} ) $.
If in addition the mapping $ F : W \rightarrow Z $ is continuously differentiable on $ W $, if the implicit function $ f : U \rightarrow V $ is continuous on $ U $, $ U \times X \subset W $, and if for any $ x \in U $ the partial Fréchet derivative $ F _ {y} ( x , f ( x) ) $ is an invertible element of $ {\mathcal L} ( \mathbf Y , \mathbf Z ) $, then $ f $ is a continuously-differentiable mapping of $ U $ into $ V $.
In the general case one can also indicate conditions for the existence and the uniqueness of the implicit function in terms of the continuity of the Fréchet derivative: If $ Z $ is complete, if the mapping $ F : W \rightarrow Z $ is continuously differentiable on $ W $, if $ F ( x _ {0} , y _ {0} ) = z _ {0} $, and if the partial Fréchet derivative $ F _ {y} ( x _ {0} , y _ {0} ) $ is an invertible element of $ {\mathcal L} ( \mathbf Y , \mathbf Z ) $, then (1) is uniquely solvable in a sufficiently small neighbourhood of $ ( x _ {0} , y _ {0} ) $, i.e. there exist neighbourhoods $ U $ of $ x _ {0} $ in $ X $ and $ V $ of $ y _ {0} $ in $ Y $, $ U \times V \subset W $, and a unique implicit function $ f : U \rightarrow V $ satisfying (2). Here $ f $ is also continuously differentiable on $ U $. In this form the implicit-function theorem for normed spaces is a direct generalization of the corresponding classic implicit-function theorem for a single scalar equation in two variables.
Furthermore, if $ F : W \rightarrow Z $ is a $ k $- times continuously-differentiable mapping in a neighbourhood $ W $ of $ ( x _ {0} , y _ {0} ) $, $ k = 1 , 2 \dots $ then the implicit function $ f : U \rightarrow V $ is also $ k $ times continuously differentiable.
Far-reaching generalizations of the classic implicit-function theorem to differential operators were given by J. Nash (see Nash theorems (in differential geometry)).
References
| [1] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [2] | L.A. Lyusternik, V.I. Sobolev, "Elemente der Funktionalanalysis" , Akademie Verlag (1968) (Translated from Russian) |
| [3] | S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian) |
| [4] | L. Schwartz, "Cours d'analyse" , 1 , Hermann (1967) |
| [5] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1 , MIR (1982) (Translated from Russian) |
| [a1] | W. Fleming, "Functions of several variables" , Addison-Wesley (1965) |
| [a2] | T.M. Flett, "Differential Analysis" , Cambridge University Press (1980) |
Implicit function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Implicit_function&oldid=55260