The functions given by the formulas:
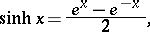 | (1) |
the hyperbolic sine; and
 | (2) |
the hyperbolic cosine. The hyperbolic tangent
is also sometimes considered. Other notations include: 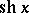 ,
, 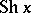 ,
, 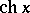 ,
, 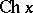 ,
, 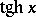 ,
, 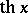 ,
, 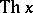 . The graphs of these functions are shown in Fig. a.
. The graphs of these functions are shown in Fig. a.
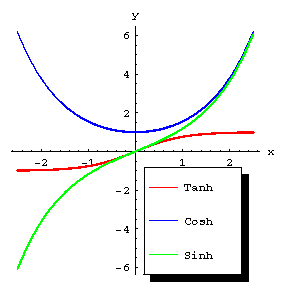
Figure: h048250a
The principal relations are:
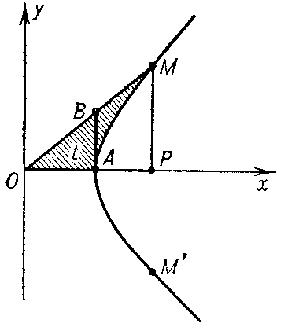
Figure: h048250b
The geometrical interpretation of hyperbolic functions is similar to that of the trigonometric functions (Fig. b). The parametric equations of hyperbolas
make it possible to interpret the abscissa 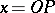 and the ordinate
and the ordinate 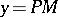 of a point
of a point 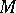 on the equilateral hyperbola
on the equilateral hyperbola 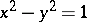 as the hyperbolic sine and cosine; the hyperbolic tangent is the segment
as the hyperbolic sine and cosine; the hyperbolic tangent is the segment 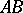 . The parameter
. The parameter 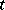 of the point
of the point 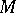 equals twice the area of the sector
equals twice the area of the sector 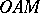 , where
, where 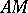 is the arc of the hyperbola. The parameter
is the arc of the hyperbola. The parameter 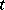 is negative for a point
is negative for a point 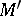 (for
(for 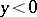 ).
).
The inverse hyperbolic functions are defined by the formulas
The derivatives and basic integrals of the hyperbolic functions are:
The hyperbolic functions 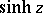 and
and 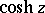 may also be defined by the series
may also be defined by the series
in the entire complex  -plane, so that
-plane, so that
 | (3) |
Extensive tabulated values of hyperbolic functions are available. The values of the hyperbolic functions may also be obtained from tables giving 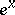 and
and 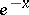 .
.
References
| [1] | E. Jahnke, F. Emde, F. Lösch, "Tafeln höheren Funktionen" , Teubner (1966) |
| [2] | , Tables of circular and hyperbolic sines and cosines in radial angle measure , Moscow (1968) (In Russian) |
| [3] | , Tables of 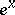 and and 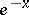 , Moscow (1955) (In Russian) , Moscow (1955) (In Russian) |
The right-hand sides of the defining relations (1), (2) allow analytic continuation to the whole complex plane. After this, using the Euler formulas one sees that (3) holds, from which the series expansions are readily derived.
References
| [a1] | A. Segun, M. Abramowitz, "Handbook of mathematical functions" , Appl. Math. Ser. , 55 , Nat. Bur. Standards (1970) |
| [a2] | H.B. Dwight, "Tables of integrals and other mathematical data" , Macmillan (1963) |
How to Cite This Entry:
Hyperbolic functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hyperbolic_functions&oldid=29142
This article was adapted from an original article by V.I. Bityutskov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article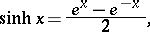

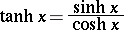
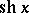 ,
, 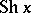 ,
, 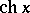 ,
, 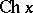 ,
, 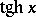 ,
, 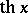 ,
, 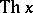 . The graphs of these functions are shown in Fig. a.
. The graphs of these functions are shown in Fig. a.

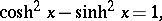
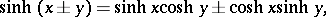
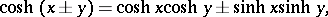

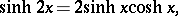
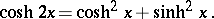
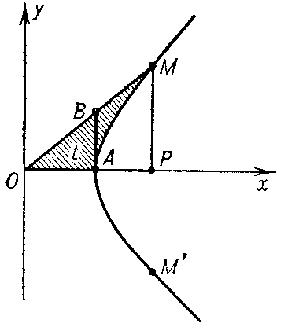

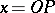 and the ordinate
and the ordinate 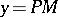 of a point
of a point 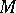 on the equilateral hyperbola
on the equilateral hyperbola 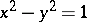 as the hyperbolic sine and cosine; the hyperbolic tangent is the segment
as the hyperbolic sine and cosine; the hyperbolic tangent is the segment 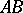 . The parameter
. The parameter 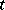 of the point
of the point 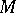 equals twice the area of the sector
equals twice the area of the sector 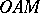 , where
, where 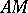 is the arc of the hyperbola. The parameter
is the arc of the hyperbola. The parameter 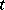 is negative for a point
is negative for a point 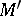 (for
(for 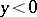 ).
).
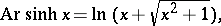
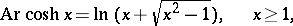
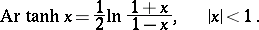

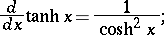
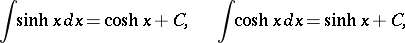
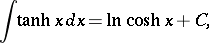
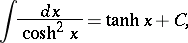
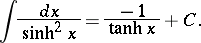
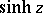 and
and 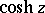 may also be defined by the series
may also be defined by the series
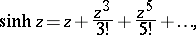
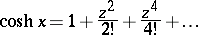
 -plane, so that
-plane, so that

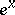 and
and 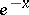 .
.
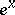 and
and 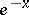 , Moscow (1955) (In Russian)
, Moscow (1955) (In Russian)