Difference between revisions of "Homology of a complex"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 2: | Line 2: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S. MacLane, "Homology" , Springer (1963) {{MR|}} {{ZBL|0818.18001}} {{ZBL|0328.18009}} </TD></TR></table> |
| Line 10: | Line 10: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) {{MR|0210112}} {{MR|1325242}} {{ZBL|0145.43303}} </TD></TR></table> |
Revision as of 21:53, 30 March 2012
The starting point for various homological constructions. Let 
be an Abelian category and let 
be a chain complex in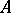 
, i.e. a family of objects 
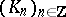in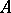 
and morphisms 
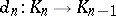such that 
for all 
. The quotient object 
is called the 
-th homology of the complex 
and is denoted by 
. The family 
is also denoted by 
. The concept of the homology of a complex serves as the base for a number of important constructions in homological algebra, commutative algebra, algebraic geometry, and topology. Thus, in topology, each topological space 
defines a chain complex in the category 
of Abelian groups: 
. Here 
is the group of 
-dimensional singular chains of 
, while 
is the boundary homomorphism. The 
-th homology of this complex is said to be the 
-th singular homology group of 
and is denoted by 
. The concept of the cohomology of a cochain complex is defined in a dual manner.
References
| [1] | S. MacLane, "Homology" , Springer (1963) Zbl 0818.18001 Zbl 0328.18009 |
Comments
References
| [a1] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) MR0210112 MR1325242 Zbl 0145.43303 |
Homology of a complex. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Homology_of_a_complex&oldid=14116