Difference between revisions of "Holomorphy, criteria for"
(Importing text file) |
m |
||
| Line 1: | Line 1: | ||
''criteria for analyticity'' | ''criteria for analyticity'' | ||
| − | The natural criteria for holomorphy (analyticity) of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h120/h120110/h1201101.png" /> (or continuous) function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h120/h120110/h1201102.png" /> in a domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h120/h120110/h1201103.png" /> of the complex plane are "infinitesimal" (cf. [[Analytic function|Analytic function]]), namely: power series expansions, the [[ | + | The natural criteria for holomorphy (analyticity) of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h120/h120110/h1201101.png" /> (or continuous) function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h120/h120110/h1201102.png" /> in a domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h120/h120110/h1201103.png" /> of the complex plane are "infinitesimal" (cf. [[Analytic function|Analytic function]]), namely: power series expansions, the [[Cauchy-Riemann equations]], and even the [[Morera theorem|Morera theorem]], since it states that |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h120/h120110/h1201104.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h120/h120110/h1201104.png" /></td> </tr></table> | ||
Revision as of 13:37, 26 December 2013
criteria for analyticity
The natural criteria for holomorphy (analyticity) of a 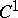 (or continuous) function
(or continuous) function 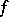 in a domain
in a domain  of the complex plane are "infinitesimal" (cf. Analytic function), namely: power series expansions, the Cauchy-Riemann equations, and even the Morera theorem, since it states that
of the complex plane are "infinitesimal" (cf. Analytic function), namely: power series expansions, the Cauchy-Riemann equations, and even the Morera theorem, since it states that
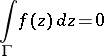 |
for all Jordan curves 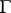 such that
such that 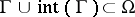 , is a necessary and sufficient condition for
, is a necessary and sufficient condition for 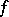 being analytic in
being analytic in  . The condition (and the usual proofs) depend on the fact that
. The condition (and the usual proofs) depend on the fact that 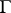 can be taken to be arbitrarily small.
can be taken to be arbitrarily small.
The first "non-infinitesimal" condition is due to M. Agranovsky and R.E. Val'skii (see [a2] and [a6] for all relevant references): Let 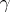 be a piecewise smooth Jordan curve, then a function
be a piecewise smooth Jordan curve, then a function 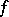 continuous in
continuous in 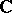 is entire (analytic everywhere) if and only if for every transformation
is entire (analytic everywhere) if and only if for every transformation 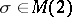 and
and 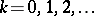 it satisfies
it satisfies
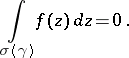 |
(Recall that 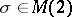 means that
means that 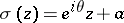 ,
, 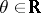 ,
, 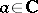 .)
.)
A generalization of this theorem and of Morera's theorem which is both local and non-infinitesimal is the following Berenstein–Gay theorem [a3].
Let 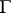 be a Jordan polygon contained in
be a Jordan polygon contained in 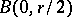 and
and 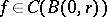 ; then
; then 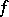 is analytic in
is analytic in 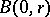 if and only if for any
if and only if for any 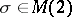 such that
such that 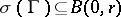 ,
,
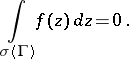 |
This theorem can be extended to several complex variables and other geometries (see [a2], [a5], and [a6] for references).
A different kind of conditions for holomorphy occur when one considers the problem of extending a continuous function defined on a curve in 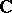 (or in a real
(or in a real 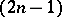 -manifold in
-manifold in 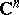 ) to an analytic function defined in a domain that contains the curve (or hypersurface) on its boundary. This is sometimes called a CR extension. An example of this type, generalizing the moment conditions of the Berenstein–Gay theorem, appears in the work of L. Aizenberg and collaborators (cf. also Analytic continuation into a domain of a function given on part of the boundary; Carleman formulas): Let
) to an analytic function defined in a domain that contains the curve (or hypersurface) on its boundary. This is sometimes called a CR extension. An example of this type, generalizing the moment conditions of the Berenstein–Gay theorem, appears in the work of L. Aizenberg and collaborators (cf. also Analytic continuation into a domain of a function given on part of the boundary; Carleman formulas): Let 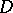 be a subdomain of
be a subdomain of 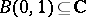 , bounded by an arc of the unit circle and a smooth simple curve
, bounded by an arc of the unit circle and a smooth simple curve 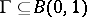 and assume that
and assume that 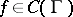 . Then there is a function
. Then there is a function 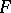 , holomorphic inside
, holomorphic inside 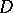 and continuous on its closure, such that
and continuous on its closure, such that 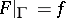 if and only if
if and only if
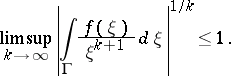 |
A boundary version of the Berenstein–Gay theorem can be proven when regarding the Heisenberg group 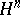 (cf. also Nil manifold) as the boundary of the Siegel upper half-space
(cf. also Nil manifold) as the boundary of the Siegel upper half-space
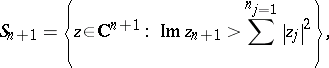 |
but the boundary values are restricted to be in 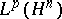 ,
, 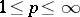 , [a1]. Related analytic extension theorems from continuous boundary values have been proven by J. Globevnik and E.L. Stout, E. Grinberg, W. Rudin, and others (see [a2] for references) in the bounded "version" of
, [a1]. Related analytic extension theorems from continuous boundary values have been proven by J. Globevnik and E.L. Stout, E. Grinberg, W. Rudin, and others (see [a2] for references) in the bounded "version" of  , namely the unit ball
, namely the unit ball 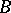 of
of 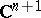 , or, more generally, for bounded domains, by essentially considering extensions from the boundary to complex subspaces. An example is the following Globevnik–Stout theorem, [a4].
, or, more generally, for bounded domains, by essentially considering extensions from the boundary to complex subspaces. An example is the following Globevnik–Stout theorem, [a4].
Let  be a bounded domain in
be a bounded domain in 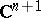 with
with 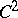 boundary. Let
boundary. Let 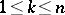 and assume
and assume 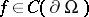 is such that
is such that
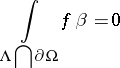 |
for all complex 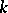 -planes intersecting
-planes intersecting 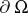 transversally, and all
transversally, and all 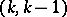 -forms
-forms 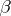 with constant coefficients. Then
with constant coefficients. Then 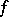 is a
is a 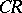 -function, i.e. has an extension as an analytic function to
-function, i.e. has an extension as an analytic function to  .
.
References
| [a1] | M. Agranovsky, C. Berenstein, D.C. Chang, "Morera theorem for holomorphic 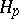 functions in the Heisenberg group" J. Reine Angew. Math. , 443 (1993) pp. 49–89 functions in the Heisenberg group" J. Reine Angew. Math. , 443 (1993) pp. 49–89 |
| [a2] | C. Berenstein, D.C. Chang, D. Pascuas, L. Zalcman, "Variations on the theorem of Morera" Contemp. Math. , 137 (1992) pp. 63–78 |
| [a3] | C. Berenstein, R. Gay, "Le probléme de Pompeiu local" J. Anal. Math. , 52 (1988) pp. 133–166 |
| [a4] | J. Globevnik, E.L. Stout, "Boundary Morera theorems for holomorphic functions of several complex variables" Duke Math. J. , 64 (1991) pp. 571–615 |
| [a5] | L. Zalcman, "Offbeat integral geometry" Amer. Math. Monthly , 87 (1980) pp. 161–175 |
| [a6] | L. Zalcman, "A bibliographic survey of the Pompeiu problem" B. Fuglede (ed.) et al. (ed.) , Approximation by Solutions of Partial Differential equations , Kluwer Acad. Publ. (1992) pp. 185–194 |
Holomorphy, criteria for. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Holomorphy,_criteria_for&oldid=14210