Hermitian operator
From Encyclopedia of Mathematics
symmetric operator
A linear operator  on a Hilbert space
on a Hilbert space  with a dense domain of definition
with a dense domain of definition  and such that
and such that  for any
for any  . This condition is equivalent to: 1)
. This condition is equivalent to: 1)  ; and 2)
; and 2)  for all
for all  , where
, where  is the adjoint of
is the adjoint of 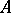 , that is, to
, that is, to 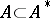 . A bounded Hermitian operator is either defined on the whole of
. A bounded Hermitian operator is either defined on the whole of 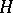 or can be so extended by continuity, and then
or can be so extended by continuity, and then 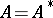 , that is,
, that is, 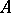 is a self-adjoint operator. An unbounded Hermitian operator may or may not have self-adjoint extensions. Sometimes any self-adjoint operator is called Hermitian, preserving the name symmetric for an operator that is Hermitian in the sense explained above. On a finite-dimensional space a Hermitian operator can be described by a Hermitian matrix.
is a self-adjoint operator. An unbounded Hermitian operator may or may not have self-adjoint extensions. Sometimes any self-adjoint operator is called Hermitian, preserving the name symmetric for an operator that is Hermitian in the sense explained above. On a finite-dimensional space a Hermitian operator can be described by a Hermitian matrix.
References
| [1] | N.I. Akhiezer, I.M. Glazman, "Theory of linear operators in Hilbert space" , 1–2 , Pitman (1981) (Translated from Russian) |
| [2] | F. Riesz, B. Szökefalvi-Nagy, "Functional analysis" , F. Ungar (1955) (Translated from French) |
How to Cite This Entry:
Hermitian operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hermitian_operator&oldid=13375
Hermitian operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hermitian_operator&oldid=13375
This article was adapted from an original article by V.I. Sobolev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article